目标
给你一个大小为 n x n 的整数方阵 grid。返回一个经过如下调整的矩阵:
- 左下角三角形(包括中间对角线)的对角线按 非递增顺序 排序。
- 右上角三角形 的对角线按 非递减顺序 排序。
示例 1:
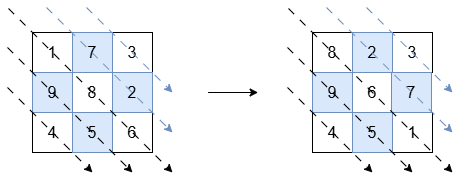
输入: grid = [[1,7,3],[9,8,2],[4,5,6]]
输出: [[8,2,3],[9,6,7],[4,5,1]]
解释:
标有黑色箭头的对角线(左下角三角形)应按非递增顺序排序:
[1, 8, 6] 变为 [8, 6, 1]。
[9, 5] 和 [4] 保持不变。
标有蓝色箭头的对角线(右上角三角形)应按非递减顺序排序:
[7, 2] 变为 [2, 7]。
[3] 保持不变。示例 2:

输入: grid = [[0,1],[1,2]]
输出: [[2,1],[1,0]]
解释:
标有黑色箭头的对角线必须按非递增顺序排序,因此 [0, 2] 变为 [2, 0]。其他对角线已经符合要求。示例 3:
输入: grid = [[1]]
输出: [[1]]
解释:
只有一个元素的对角线已经符合要求,因此无需修改。说明:
- grid.length == grid[i].length == n
- 1 <= n <= 10
-10^5 <= grid[i][j] <= 10^5
思路
参考 498.对角线遍历
代码
/**
* @date 2025-08-28 8:57
*/
public class SortMatrix3446 {
public int[][] sortMatrix(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int k = m + n - 1;
for (int l = 1; l < n; l++) {
int maxJ = Math.min(m + n - l - 1, n - 1);
int minJ = Math.max(0, n - l);
List<Integer> list = new ArrayList<>();
for (int j = minJ; j <= maxJ; j++) {
int i = j + l - n;
list.add(grid[i][j]);
}
list.sort(null);
int p = 0;
for (int j = minJ; j <= maxJ; j++) {
int i = j + l - n;
grid[i][j] = list.get(p++);
}
}
for (int l = n; l <= k; l++) {
int maxJ = Math.min(m + n - l - 1, n - 1);
int minJ = Math.max(0, n - l);
List<Integer> list = new ArrayList<>();
for (int j = minJ; j <= maxJ; j++) {
int i = j + l - n;
list.add(grid[i][j]);
}
list.sort(Collections.reverseOrder());
int p = 0;
for (int j = minJ; j <= maxJ; j++) {
int i = j + l - n;
grid[i][j] = list.get(p++);
}
}
return grid;
}
}
性能