日期: 2026年1月19日

目标

给你一个大小为 m x n 的矩阵 mat 和一个整数阈值 threshold。

请你返回元素总和小于或等于阈值的正方形区域的最大边长；如果没有这样的正方形区域，则返回 0 。

示例 1：

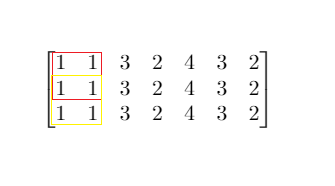
输入：mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
输出：2
解释：总和小于或等于 4 的正方形的最大边长为 2，如图所示。

示例 2：

输入：mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
输出：0

说明：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 300
• 0 <= mat[i][j] <= 10^4
• 0 <= threshold <= 10^5

思路

有一个 m x n 矩阵，返回其中元素和不超过 threshold 的正方形的最大边长。

使用二维前缀和计算面积，枚举右下顶点与边长，边长从已知的最大值开始枚举，超出 threshold 就退出循环，时间复杂度为 O(mn + min(m, n))。

代码

/**
 * @date 2026-01-19 9:46
 */
public class MaxSideLength1292 {

    public int maxSideLength_v1(int[][] mat, int threshold) {
        int m = mat.length;
        int n = mat[0].length;
        int[][] prefix = new int[m + 1][n + 1];
        int res = 0;
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                prefix[i][j] = prefix[i][j - 1] + mat[i - 1][j - 1] + prefix[i - 1][j] - prefix[i - 1][j - 1];
                int l = Math.min(i, j);
                for (int k = res + 1; k <= l; k++) {
                    int area = prefix[i][j] - prefix[i - k][j] - prefix[i][j - k] + prefix[i - k][j - k];
                    if (area <= threshold) {
                        res = Math.max(res, k);
                    } else {
                        break;
                    }
                }
            }
        }
        return res;
    }

}

性能