目标
平面上有 n 个点,点的位置用整数坐标表示 points[i] = [xi, yi] 。请你计算访问所有这些点需要的 最小时间(以秒为单位)。
你需要按照下面的规则在平面上移动:
- 每一秒内,你可以:
- 沿水平方向移动一个单位长度,或者
- 沿竖直方向移动一个单位长度,或者
- 跨过对角线移动 sqrt(2) 个单位长度(可以看作在一秒内向水平和竖直方向各移动一个单位长度)。
- 必须按照数组中出现的顺序来访问这些点。
- 在访问某个点时,可以经过该点后面出现的点,但经过的那些点不算作有效访问。
示例 1:
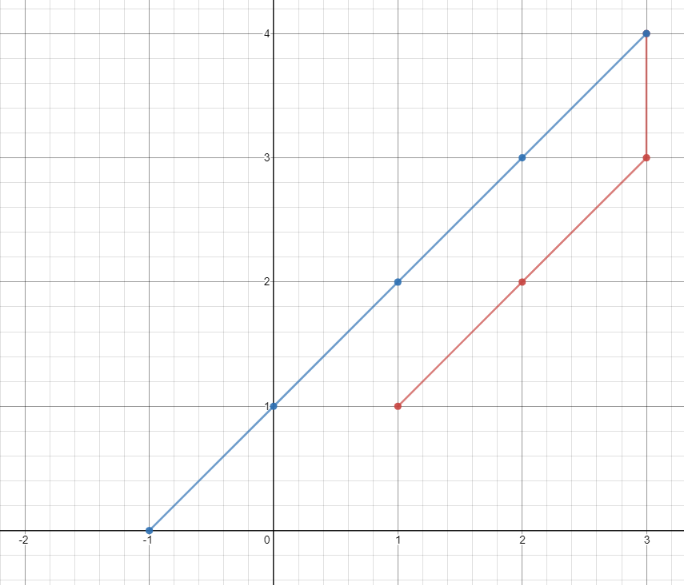
输入:points = [[1,1],[3,4],[-1,0]]
输出:7
解释:一条最佳的访问路径是: [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]
从 [1,1] 到 [3,4] 需要 3 秒
从 [3,4] 到 [-1,0] 需要 4 秒
一共需要 7 秒示例 2:
输入:points = [[3,2],[-2,2]]
输出:5说明:
- points.length == n
- 1 <= n <= 100
- points[i].length == 2
- -1000 <= points[i][0], points[i][1] <= 1000
思路
二维平面上有一些点 points,按顺序访问这些点,每一秒可以沿 x 轴、 y 轴 或者 格子的对角线移动,求访问所有点的最小时间。
优先走斜线,直到与下一个坐标点的 横坐标 或者 纵坐标 相等,然后再走直线。两点之间最短时间为 Math.max(dx, dy),即切比雪夫距离。
代码
/**
* @date 2026-01-12 8:50
*/
public class MinTimeToVisitAllPoints1266 {
public int minTimeToVisitAllPoints(int[][] points) {
int res = 0;
for (int i = 1; i < points.length; i++) {
int dx = Math.abs(points[i][0] - points[i - 1][0]);
int dy = Math.abs(points[i][1] - points[i - 1][1]);
res += Math.max(dx, dy);
}
return res;
}
}
性能