目标
3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。
给定一个由整数组成的row x col 的 grid,其中有多少个 3 × 3 的 “幻方” 子矩阵?
注意:虽然幻方只能包含 1 到 9 的数字,但 grid 可以包含最多15的数字。
示例 1:
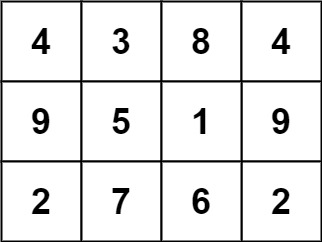
输入: grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2]
输出: 1
解释:
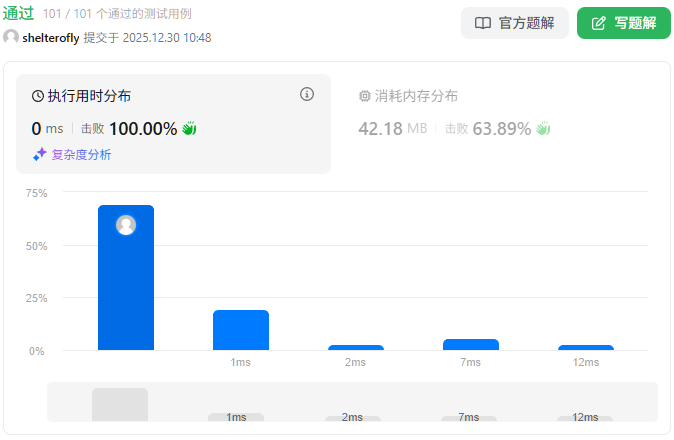
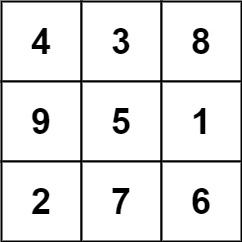
下面的子矩阵是一个 3 x 3 的幻方:
而这一个不是:
总的来说,在本示例所给定的矩阵中只有一个 3 x 3 的幻方子矩阵。
示例 2:
输入: grid = [[8]]
输出: 0说明:
- row == grid.length
- col == grid[i].length
- 1 <= row, col <= 10
- 0 <= grid[i][j] <= 15
思路
判断给定矩阵中幻方的数量,幻方是一个九宫格,元素为 1 ~ 9 且行/列/对角线的元素和相等。
如果数字是 1 ~ 9,所有元素和为 45,幻方和为 sum / 3 = 15。将过中心的四条线相加,刚好等于 sum + 3 * center = 4 * 15 = 60,求得 center = 5。
使用 mask 记录出现过的数字,全部出现的二进制表示为 1111111110,即 2^10 - 1 - 1。
在保证数字是 1 ~ 9 的前提下,如果判断了前两行满足条件,则无需判断最后一行,同理,如果判断了前两列满足条件,无需判断最后一列。因为总和是 45,剩余的行/列和等于 45 - 30 = 15。在此基础上,对角线也无需判断,由于中间元素是 5,对角和一定是 10。
a b c
d e f
g h i由于行/列和为 15,那么 b + h = d + f = 10。1 ~ 9 范围内和为 10 的组合只有四种 1 9,2 8,3 7,4 6。剩余四个位置 a c g i,如果对角和不等于 10,有 a + c 或 a + g 等于 10,但是 b 与 d 不可能为 5,矛盾。而如果 a i 和为 10,剩余的 c g 和也为 10。
代码
/**
* @date 2025-12-30 9:10
*/
public class NumMagicSquaresInside840 {
public int numMagicSquaresInside(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
if (m < 3 || n < 3) {
return 0;
}
int res = 0;
for (int i = 1; i < m - 1; i++) {
for (int j = 1; j < n - 1; j++) {
if (check(grid, i, j)) {
res++;
}
}
}
return res;
}
public boolean check(int[][] grid, int i, int j) {
if (grid[i][j] != 5) {
return false;
}
int[] rowSum = new int[3];
int[] colSum = new int[3];
int mask = 0;
int r = 0;
for (int row = i - 1; row <= i + 1; row++) {
int c = 0;
for (int col = j - 1; col <= j + 1; col++) {
rowSum[r] += grid[row][col];
colSum[c++] += grid[row][col];
mask |= 1 << grid[row][col];
}
r++;
}
return rowSum[0] == 15 && rowSum[1] == 15 && colSum[0] == 15 && colSum[1] == 15 && mask == (1 << 10) - 2;
}
}
性能