目标
在一个图书馆的长廊里,有一些座位和装饰植物排成一列。给你一个下标从 0 开始,长度为 n 的字符串 corridor ,它包含字母 'S' 和 'P' ,其中每个 'S' 表示一个座位,每个 'P' 表示一株植物。
在下标 0 的左边和下标 n - 1 的右边 已经 分别各放了一个屏风。你还需要额外放置一些屏风。每一个位置 i - 1 和 i 之间(1 <= i <= n - 1),至多能放一个屏风。
请你将走廊用屏风划分为若干段,且每一段内都 恰好有两个座位 ,而每一段内植物的数目没有要求。可能有多种划分方案,如果两个方案中有任何一个屏风的位置不同,那么它们被视为 不同 方案。
请你返回划分走廊的方案数。由于答案可能很大,请你返回它对 10^9 + 7 取余 的结果。如果没有任何方案,请返回 0 。
示例 1:
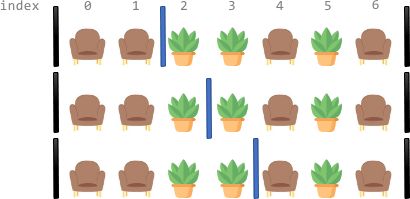
输入:corridor = "SSPPSPS"
输出:3
解释:总共有 3 种不同分隔走廊的方案。
上图中黑色的竖线表示已经放置好的屏风。
上图每种方案中,每一段都恰好有 两个 座位。示例 2:

输入:corridor = "PPSPSP"
输出:1
解释:只有 1 种分隔走廊的方案,就是不放置任何屏风。
放置任何的屏风都会导致有一段无法恰好有 2 个座位。示例 3:
输入:corridor = "S"
输出:0
解释:没有任何方案,因为总是有一段无法恰好有 2 个座位。说明:
- n == corridor.length
- 1 <= n <= 10^5
- corridor[i] 要么是 'S' ,要么是 'P' 。
思路
有一个仅由 S 与 P 组成的长廊布局示意图 corridor,其中 S 表示座位,P 表示植物, 位置 0 的左边与 n - 1 的右边已经放置了一个屏风。现在需要使用屏风将走廊进行划分,要求屏风之间只能有两个座位,求可行的划分方案数。
首先找到第二个座位的下标,再找到下一个两个座位的第一个座位的下标,它们之间的植物数量 + 1 就是可插入的屏风方案,使用乘法原理计算总方案数。
代码
/**
* @date 2025-12-22 16:28
*/
public class NumberOfWays2147 {
public int numberOfWays(String corridor) {
int mod = 1000000007;
int[] prev = new int[]{-1, 0};
int i = 0;
char[] chars = corridor.toCharArray();
int n = chars.length;
while (i < n && chars[i] == 'P') {
i++;
}
prev[1] = i - 1;
long res = 0L;
long prevCnt = 1L;
while (i < n) {
int[] cur = new int[2];
int cnt = 0;
while (i < n && cnt < 2) {
if (chars[i] == 'S') {
cur[cnt++] = i;
}
i++;
}
if (cnt == 2) {
prevCnt = (prevCnt * (cur[0] - prev[1])) % mod;
res = prevCnt;
prev = cur;
} else if (cnt == 1) {
res = 0;
}
}
return (int) res;
}
}
性能