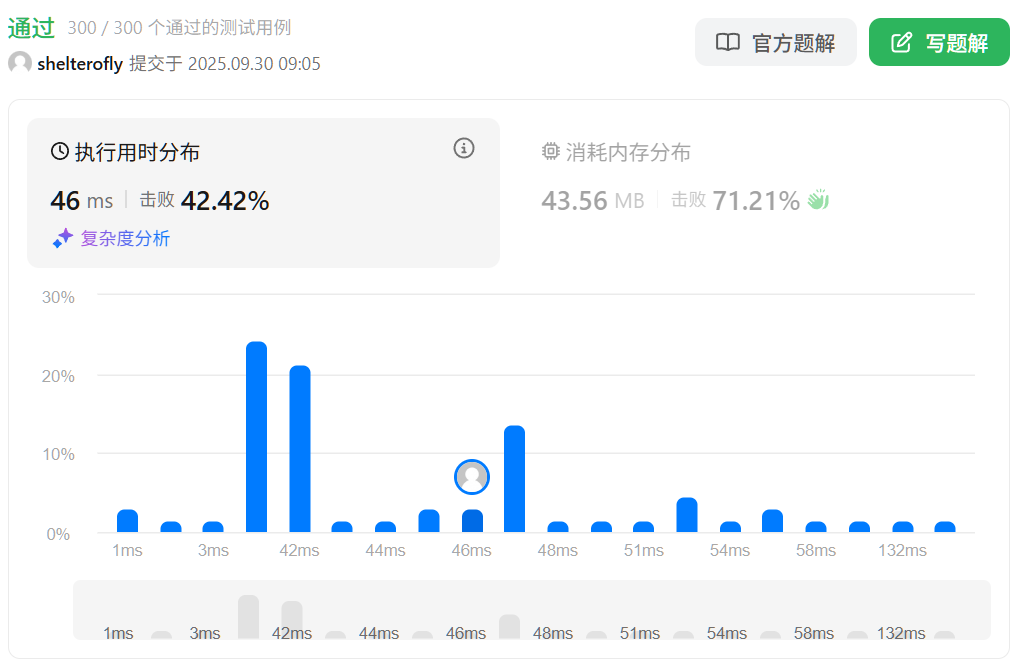
目标
你有一个电影租借公司和 n 个电影商店。你想要实现一个电影租借系统,它支持查询、预订和返还电影的操作。同时系统还能生成一份当前被借出电影的报告。
所有电影用二维整数数组 entries 表示,其中 entries[i] = [shopi, moviei, pricei] 表示商店 shopi 有一份电影 moviei 的拷贝,租借价格为 pricei 。每个商店有 至多一份 编号为 moviei 的电影拷贝。
系统需要支持以下操作:
- Search:找到拥有指定电影且 未借出 的商店中 最便宜的 5 个 。商店需要按照 价格 升序排序,如果价格相同,则 shopi 较小 的商店排在前面。如果查询结果少于 5 个商店,则将它们全部返回。如果查询结果没有任何商店,则返回空列表。
- Rent:从指定商店借出指定电影,题目保证指定电影在指定商店 未借出 。
- Drop:在指定商店返还 之前已借出 的指定电影。
- Report:返回 最便宜的 5 部已借出电影 (可能有重复的电影 ID),将结果用二维列表 res 返回,其中 res[j] = [shopj, moviej] 表示第 j 便宜的已借出电影是从商店 shopj 借出的电影 moviej 。res 中的电影需要按 价格 升序排序;如果价格相同,则 shopj 较小 的排在前面;如果仍然相同,则 moviej 较小 的排在前面。如果当前借出的电影小于 5 部,则将它们全部返回。如果当前没有借出电影,则返回一个空的列表。
请你实现 MovieRentingSystem 类:
- MovieRentingSystem(int n, int[][] entries) 将 MovieRentingSystem 对象用 n 个商店和 entries 表示的电影列表初始化。
List<Integer> search(int movie) 如上所述,返回 未借出 指定 movie 的商店列表。- void rent(int shop, int movie) 从指定商店 shop 借出指定电影 movie 。
- void drop(int shop, int movie) 在指定商店 shop 返还之前借出的电影 movie 。
List<List<Integer>> report() 如上所述,返回最便宜的 已借出 电影列表。
注意:测试数据保证 rent 操作中指定商店拥有 未借出 的指定电影,且 drop 操作指定的商店 之前已借出 指定电影。
示例 1:
输入:
["MovieRentingSystem", "search", "rent", "rent", "report", "drop", "search"]
[[3, [[0, 1, 5], [0, 2, 6], [0, 3, 7], [1, 1, 4], [1, 2, 7], [2, 1, 5]]], [1], [0, 1], [1, 2], [], [1, 2], [2]]
输出:
[null, [1, 0, 2], null, null, [[0, 1], [1, 2]], null, [0, 1]]
解释:
MovieRentingSystem movieRentingSystem = new MovieRentingSystem(3, [[0, 1, 5], [0, 2, 6], [0, 3, 7], [1, 1, 4], [1, 2, 7], [2, 1, 5]]);
movieRentingSystem.search(1); // 返回 [1, 0, 2] ,商店 1,0 和 2 有未借出的 ID 为 1 的电影。商店 1 最便宜,商店 0 和 2 价格相同,所以按商店编号排序。
movieRentingSystem.rent(0, 1); // 从商店 0 借出电影 1 。现在商店 0 未借出电影编号为 [2,3] 。
movieRentingSystem.rent(1, 2); // 从商店 1 借出电影 2 。现在商店 1 未借出的电影编号为 [1] 。
movieRentingSystem.report(); // 返回 [[0, 1], [1, 2]] 。商店 0 借出的电影 1 最便宜,然后是商店 1 借出的电影 2 。
movieRentingSystem.drop(1, 2); // 在商店 1 返还电影 2 。现在商店 1 未借出的电影编号为 [1,2] 。
movieRentingSystem.search(2); // 返回 [0, 1] 。商店 0 和 1 有未借出的 ID 为 2 的电影。商店 0 最便宜,然后是商店 1 。
说明:
- 1 <= n <= 3 * 10^5
- 1 <= entries.length <= 10^5
- 0 <= shopi < n
- 1 <= moviei, pricei <= 10^4
- 每个商店 至多 有一份电影 moviei 的拷贝。
- search,rent,drop 和 report 的调用 总共 不超过 10^5 次。
思路
代码
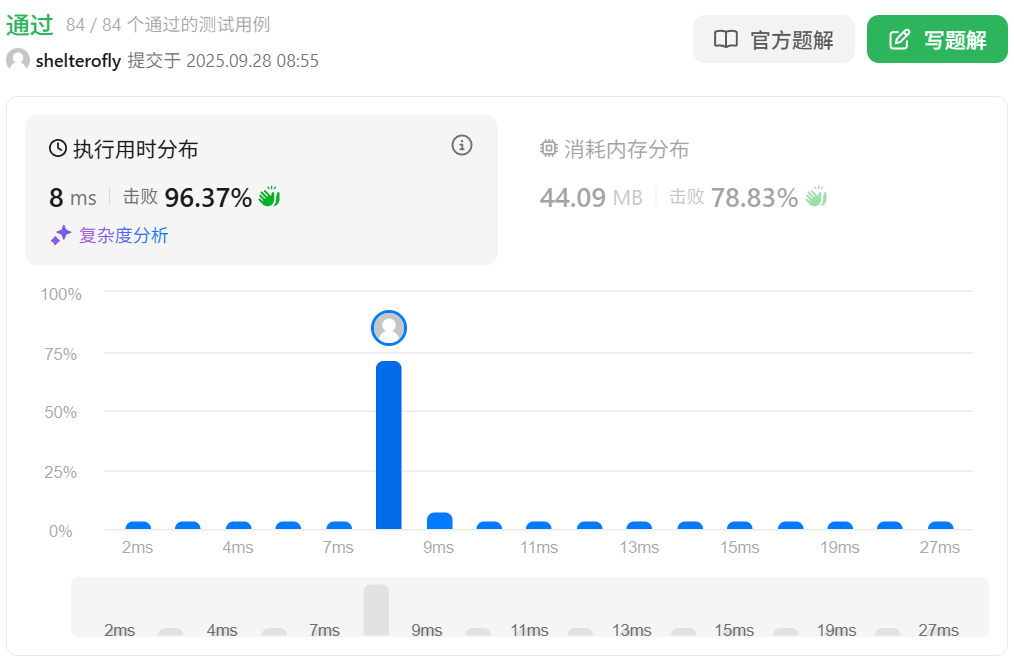
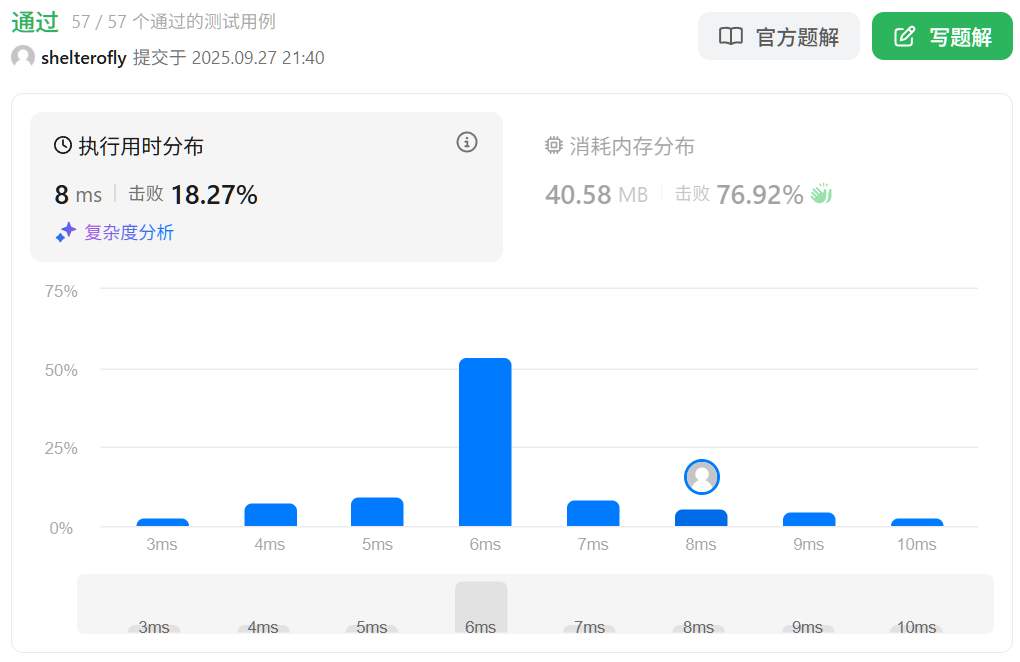
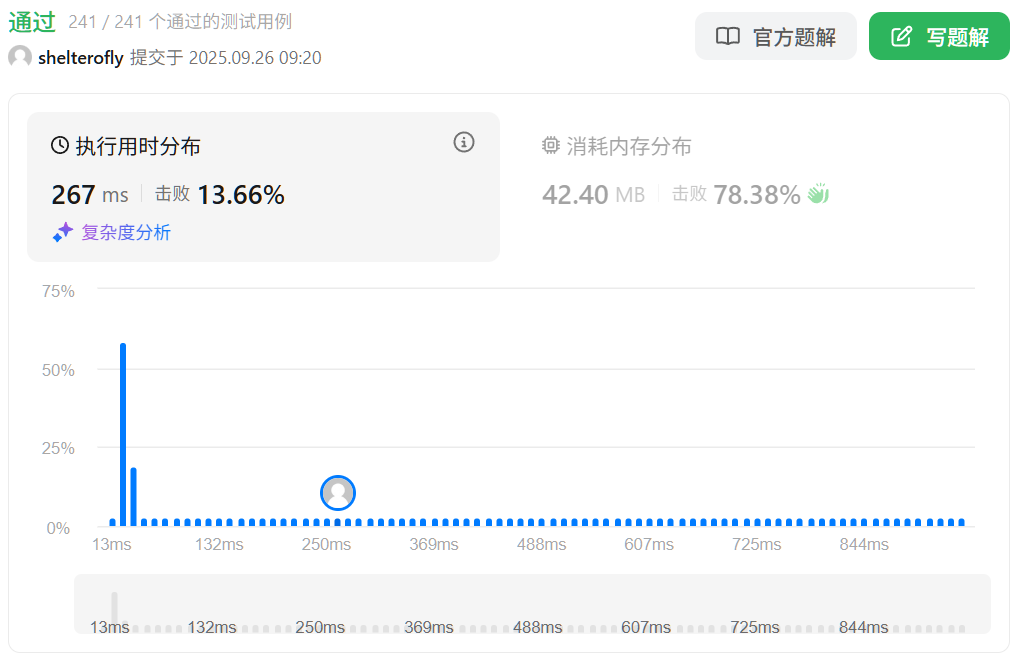
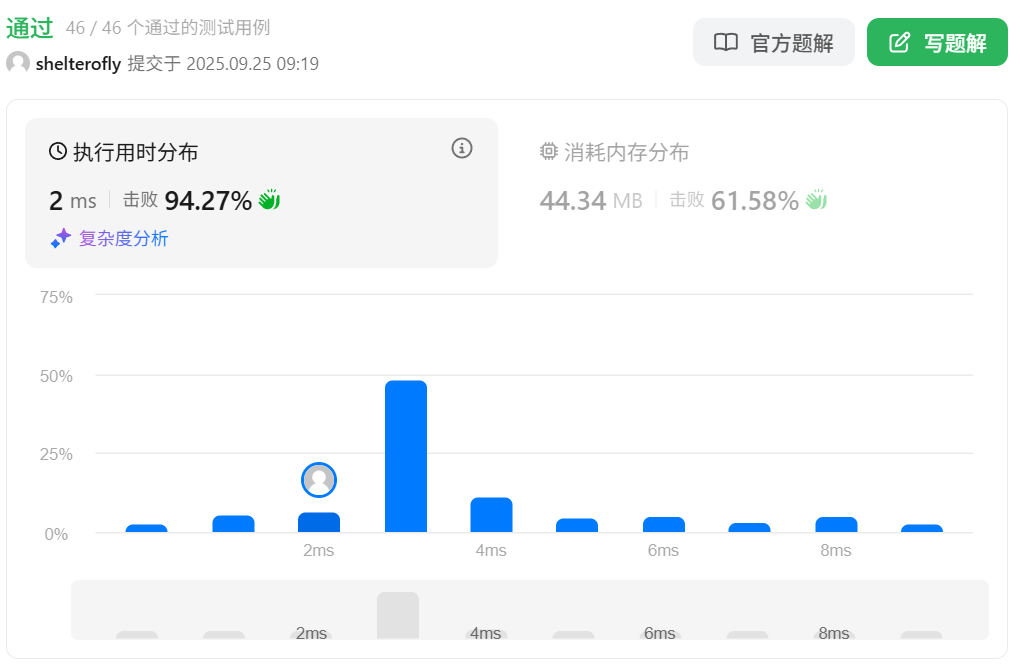
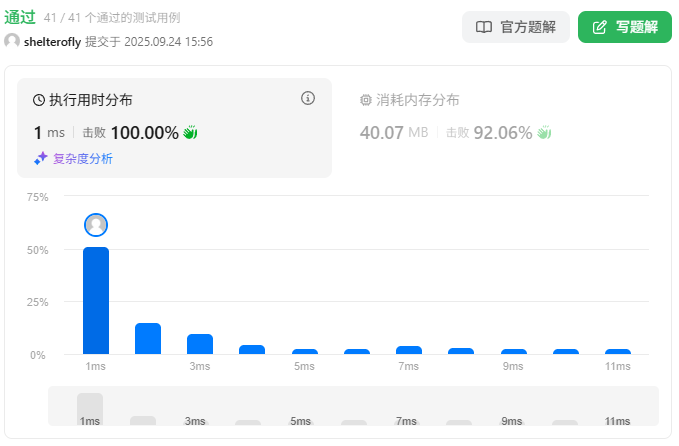
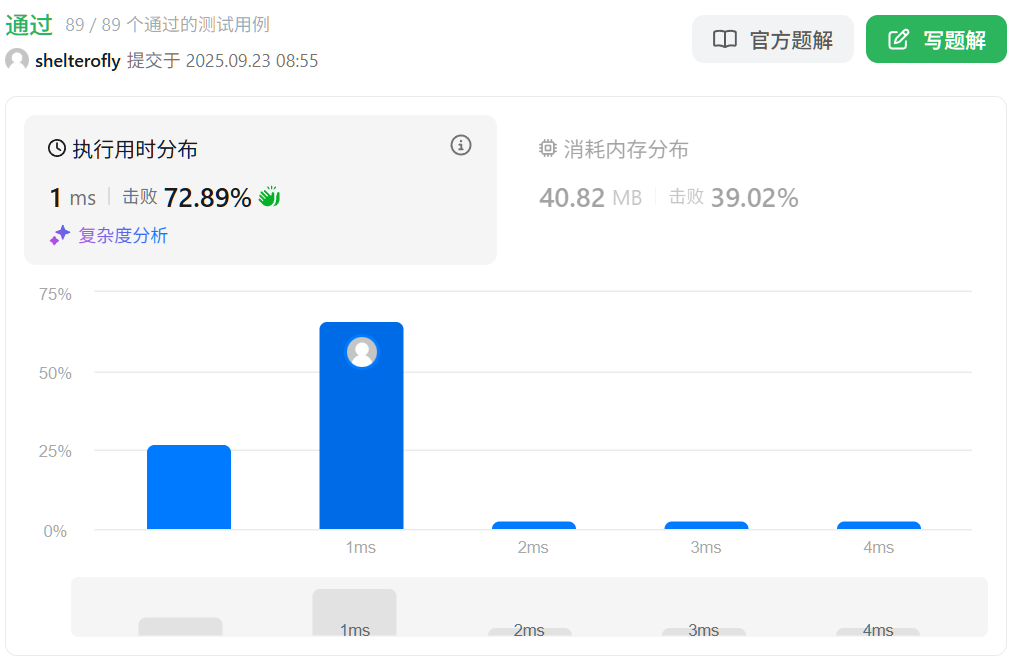
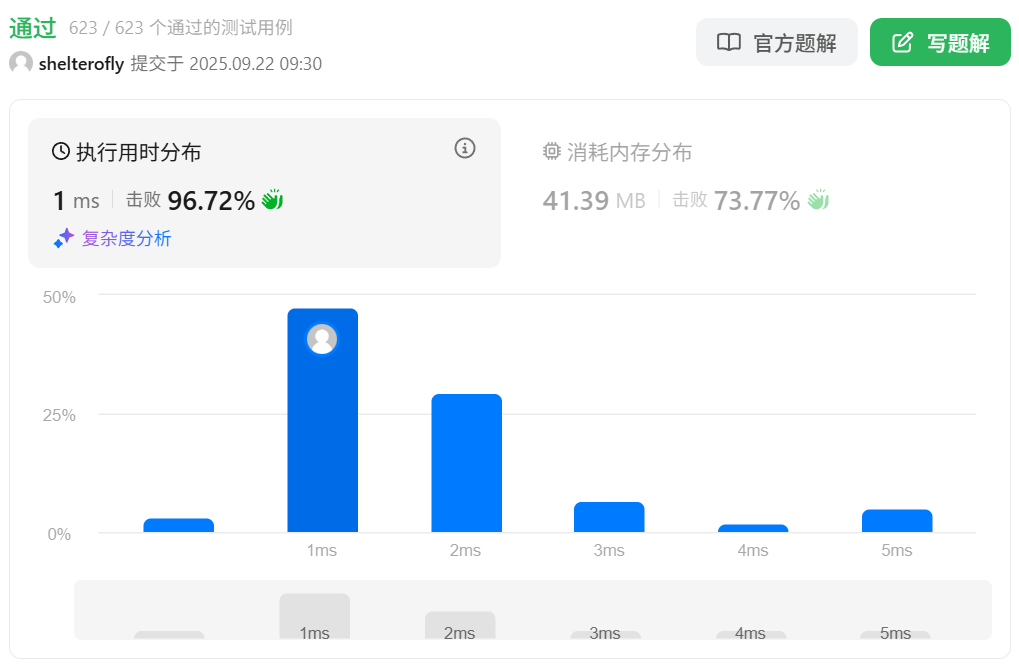
性能