日期: 2025 年 5 月 3 日

目标

在一排多米诺骨牌中，tops[i] 和 bottoms[i] 分别代表第 i 个多米诺骨牌的上半部分和下半部分。（一个多米诺是两个从 1 到 6 的数字同列平铺形成的 —— 该平铺的每一半上都有一个数字。）

我们可以旋转第 i 张多米诺，使得 tops[i] 和 bottoms[i] 的值交换。

返回能使 tops 中所有值或者 bottoms 中所有值都相同的最小旋转次数。

如果无法做到，返回 -1.

示例 1：

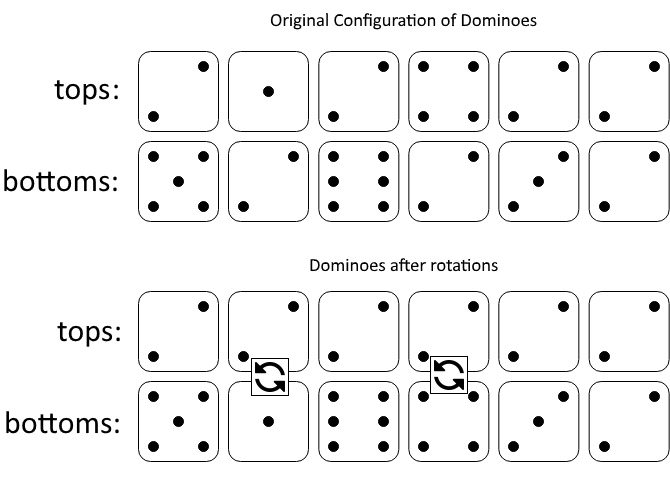
输入：tops = [2,1,2,4,2,2], bottoms = [5,2,6,2,3,2]
输出：2
解释： 
图一表示：在我们旋转之前， tops 和 bottoms 给出的多米诺牌。 
如果我们旋转第二个和第四个多米诺骨牌，我们可以使上面一行中的每个值都等于 2，如图二所示。

示例 2：

输入：tops = [3,5,1,2,3], bottoms = [3,6,3,3,4]
输出：-1
解释： 在这种情况下，不可能旋转多米诺牌使一行的值相等。

说明：

• 2 <= tops.length <= 2 * 10^4
• bottoms.length == tops.length
• 1 <= tops[i], bottoms[i] <= 6

思路

有两个长度相同的数组，数组元素 1 ~ 6，每次操作可以交换这两个数组相同下标的元素值，求使其中任意数组的元素值全部相同所需的最小操作数。

由于最终需要任一数组的元素值完全相同，不是 tops[0] 就是 bottoms[0]。分别计算将这两个数组变成这两个值的最小操作数即可。

代码

/**
 * @date 2025-05-03 20:46
 */
public class MinDominoRotations1007 {

    public int minDominoRotations_v2(int[] tops, int[] bottoms) {
        int res = Math.min(ops(tops, bottoms, tops[0]), ops(tops, bottoms, bottoms[0]));
        return res == Integer.MAX_VALUE ? -1 : res;
    }

    public int ops(int[] tops, int[] bottoms, int target) {
        int topCnt = 0;
        int bottomCnt = 0;
        for (int i = 0; i < tops.length; i++) {
            if (target != tops[i] && target != bottoms[i]) {
                return Integer.MAX_VALUE;
            }
            if (target != tops[i]) {
                topCnt++;
            } else if (target != bottoms[i]) {
                bottomCnt++;
            }
        }
        return Math.min(topCnt, bottomCnt);
    }

}

性能