日期: 2025 年 3 月 18 日

目标

给你一个下标从 0 开始的二维整数数组 nums 。

返回位于 nums 至少一条 对角线 上的最大 质数 。如果任一对角线上均不存在质数，返回 0 。

注意：

• 如果某个整数大于 1 ，且不存在除 1 和自身之外的正整数因子，则认为该整数是一个质数。
• 如果存在整数 i ，使得 nums[i][i] = val 或者 nums[i][nums.length - i - 1]= val ，则认为整数 val 位于 nums 的一条对角线上。

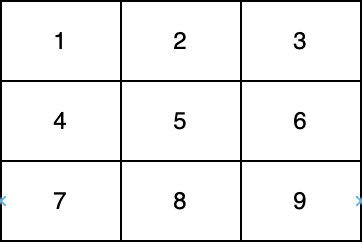
在上图中，一条对角线是 [1,5,9] ，而另一条对角线是 [3,5,7] 。

示例 1：

输入：nums = [[1,2,3],[5,6,7],[9,10,11]]
输出：11
解释：数字 1、3、6、9 和 11 是所有 "位于至少一条对角线上" 的数字。由于 11 是最大的质数，故返回 11 。

示例 2：

输入：nums = [[1,2,3],[5,17,7],[9,11,10]]
输出：17
解释：数字 1、3、9、10 和 17 是所有满足"位于至少一条对角线上"的数字。由于 17 是最大的质数，故返回 17 。

说明：

• 1 <= nums.length <= 300
• nums.length == numsi.length
• 1 <= nums[i][j] <= 4 * 10^6

思路

求 n x n 矩阵对角线上的最大质数，对角线指 (i, i) 与 (i, n - 1 - i) 上的元素。

由于本题只需判断对角线上的元素值是否是质数，总个数不超过 2n 即 600 个。可以直接枚举元素，判断元素值是否存在 1 和它本身以外的因子。

代码

/**
 * @date 2025-03-18 9:06
 */
public class DiagonalPrime2614 {

    public int diagonalPrime(int[][] nums) {
        int n = nums.length;
        int m = nums[0].length;
        int res = 0;
        for (int i = 0; i < n; i++) {
            if (nums[i][i] > res && isPrime(nums[i][i])) {
                res = nums[i][i];
            }
            if (nums[i][m - 1 - i] > res && isPrime(nums[i][m - 1 - i])) {
                res = nums[i][m - 1 - i];
            }
        }
        return res;
    }

    public boolean isPrime(int num) {
        if (num <= 1) {
            return false;
        }
        if (num <= 3) {
            return true;
        }
        if (num % 2 == 0 || num % 3 == 0) {
            return false;
        }
        for (int i = 5; i * i <= num; i += 6) {
            if (num % i == 0 || num % (i + 2) == 0) {
                return false;
            }
        }
        return true;
    }

}

性能