日期: 2025 年 3 月 11 日

目标

给你一个下标从 0 开始的整数数组 nums 。对于每个下标 i（1 <= i <= nums.length - 2），nums[i] 的 美丽值 等于：

• 2，对于所有 0 <= j < i 且 i < k <= nums.length - 1 ，满足 nums[j] < nums[i] < nums[k]
• 1，如果满足 nums[i - 1] < nums[i] < nums[i + 1] ，且不满足前面的条件
• 0，如果上述条件全部不满足

返回符合 1 <= i <= nums.length - 2 的所有 nums[i] 的 美丽值的总和 。

示例 1：

输入：nums = [1,2,3]
输出：2
解释：对于每个符合范围 1 <= i <= 1 的下标 i :
- nums[1] 的美丽值等于 2

示例 2：

输入：nums = [2,4,6,4]
输出：1
解释：对于每个符合范围 1 <= i <= 2 的下标 i :
- nums[1] 的美丽值等于 1
- nums[2] 的美丽值等于 0

示例 3：

输入：nums = [3,2,1]
输出：0
解释：对于每个符合范围 1 <= i <= 1 的下标 i :
- nums[1] 的美丽值等于 0

说明：

• 3 <= nums.length <= 10^5
• 1 <= nums[i] <= 10^5

思路

有一个数组 nums，元素的美丽值定义如下：

• 如果 nums[i] > nums[j] && 0 =< j < i && nums[i] < nums[k] && i < k <= n - 1，美丽值为 2
• 如果 nums[i - 1] < nums[i] < nums[i + 1]，美丽值为 1
• 否则美丽值为 0

简单来说就是如果元素大于它前面的所有元素值并且小于它后面的所有元素值，美丽值为 2。如果仅仅大于它前面一个元素且小于它后面一个元素，美丽值为 1。

首先想到的是使用单调栈维护当前元素后面第一个 小于等于 它的元素下标，保存到 floor[i]，如果没有记录为 n；维护当前元素前面第一个 大于等于 它的元素下标，保存到 ceiling[i]，如果没有记录为 -1。当 floor[i] == n && ceiling[i] == -1 时，美丽值为 2，floor[i] > i + 1 && ceiling[i] < i - 1 时，美丽值为 1。

网友题解使用的是维护前缀最大值和后缀最小值，如果当前元素大于前面的最大值且小于后面的最小值，美丽值为 2，否则直接比较前后两个元素，如果满足条件，美丽值为 1。

代码

/**
 * @date 2025-03-11 8:48
 */
public class SumOfBeauties2012 {

    /**
     * 前缀最大值 后缀最小值
     */
    public int sumOfBeauties_v1(int[] nums) {
        int n = nums.length;
        int[] prefix = new int[n];
        int[] suffix = new int[n];
        suffix[n - 1] = Integer.MAX_VALUE;
        for (int i = 1; i < n; i++) {
            prefix[i] = Math.max(prefix[i - 1], nums[i - 1]);
            suffix[n - 1 - i] = Math.min(suffix[n - i], nums[n - i]);
        }
        int res = 0;
        for (int i = 1; i < n - 1; i++) {
            if (nums[i] > prefix[i] && nums[i] < suffix[i]) {
                res += 2;
            } else if (nums[i] > nums[i - 1] && nums[i] < nums[i + 1]) {
                res++;
            }
        }
        return res;
    }

    /**
     * 单调栈
     */
    public int sumOfBeauties(int[] nums) {
        int n = nums.length;
        int[] floor = new int[n];
        int[] ceiling = new int[n];
        Deque<Integer> stack = new ArrayDeque<>();
        int res = 0;
        for (int i = 0; i < n; i++) {
            while (!stack.isEmpty() && nums[stack.peek()] >= nums[i]) {
                floor[stack.pop()] = i;
            }
            stack.push(i);
        }
        while (!stack.isEmpty()) {
            floor[stack.pop()] = n;
        }
        for (int i = n - 1; i >= 0; i--) {
            while (!stack.isEmpty() && nums[stack.peek()] <= nums[i]) {
                ceiling[stack.pop()] = i;
            }
            stack.push(i);
        }
        while (!stack.isEmpty()) {
            ceiling[stack.pop()] = -1;
        }
        for (int i = 1; i < n - 1; i++) {
            if (floor[i] == n && ceiling[i] == -1) {
                res += 2;
            } else if (floor[i] > i + 1 && ceiling[i] < i - 1) {
                res++;
            }
        }
        return res;
    }

}

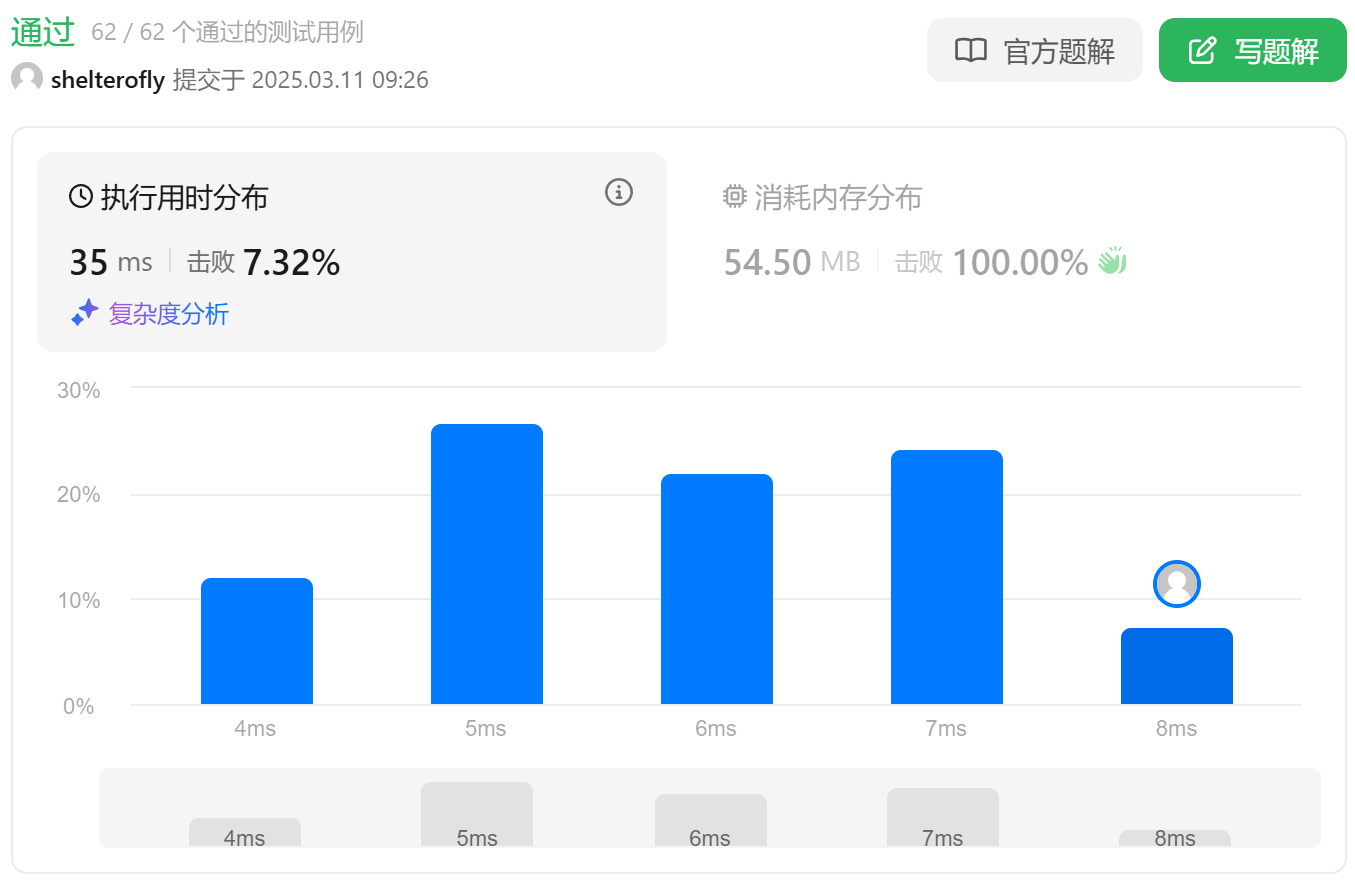
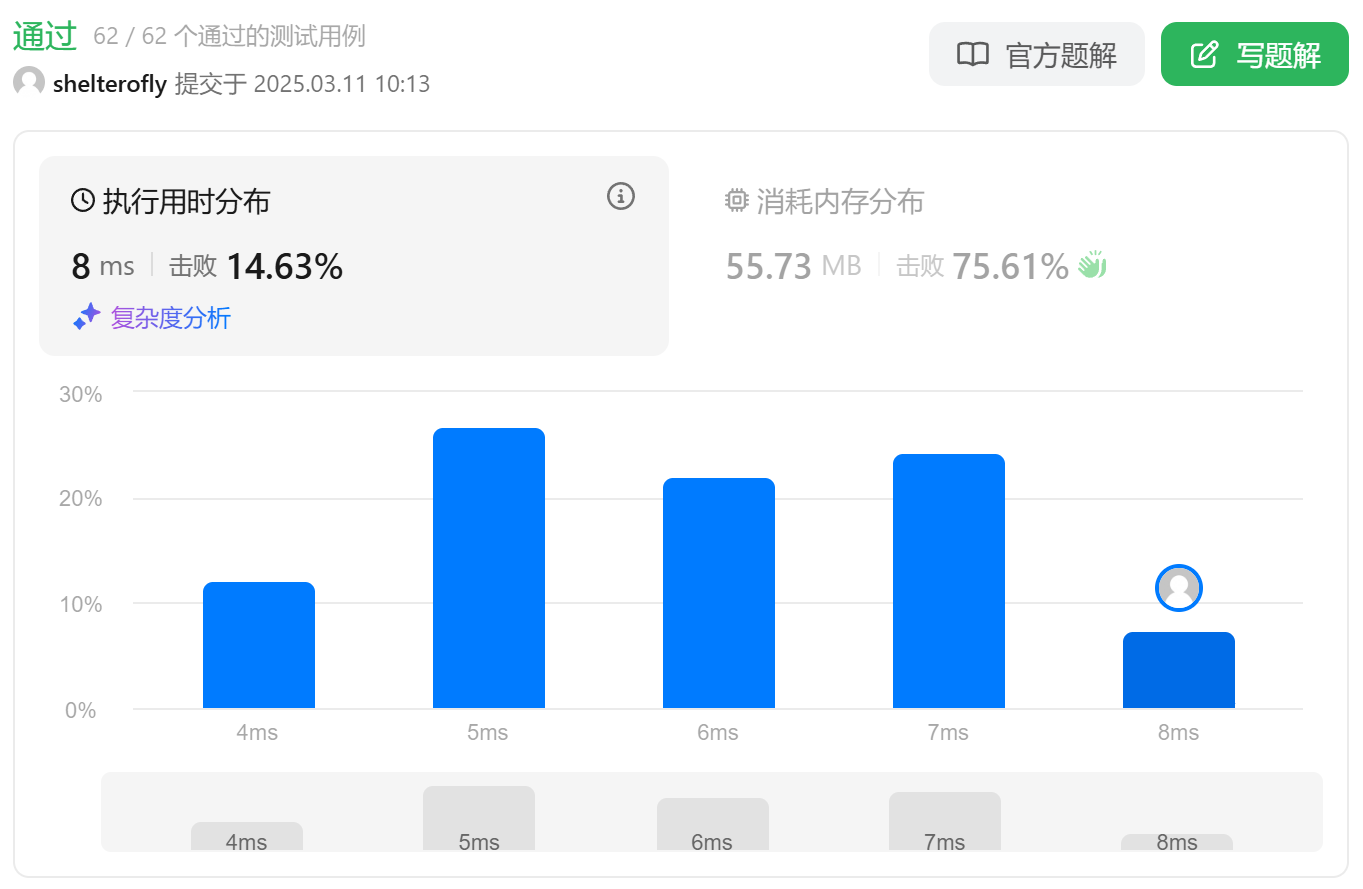
性能