目标
一个 n x n 的二维网络 board 仅由 0 和 1 组成 。每次移动,你能交换任意两列或是两行的位置。
返回 将这个矩阵变为 “棋盘” 所需的最小移动次数 。如果不存在可行的变换,输出 -1。
“棋盘” 是指任意一格的上下左右四个方向的值均与本身不同的矩阵。
示例 1:
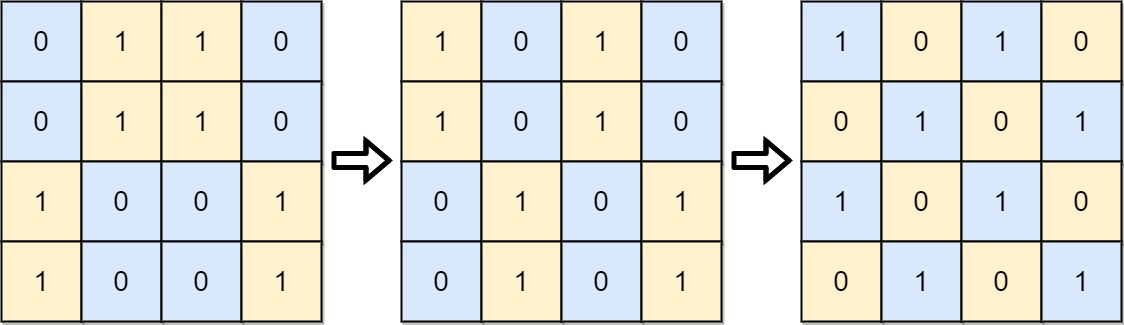
输入: board = [[0,1,1,0],[0,1,1,0],[1,0,0,1],[1,0,0,1]]
输出: 2
解释:一种可行的变换方式如下,从左到右:
第一次移动交换了第一列和第二列。
第二次移动交换了第二行和第三行。示例 2:
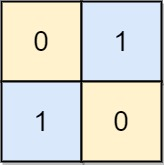
输入: board = [[0, 1], [1, 0]]
输出: 0
解释: 注意左上角的格值为0时也是合法的棋盘.示例 3:
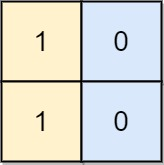
输入: board = [[1, 0], [1, 0]]
输出: -1
解释: 任意的变换都不能使这个输入变为合法的棋盘。说明:
- n == board.length
- n == board[i].length
- 2 <= n <= 30
board[i][j]将只包含 0或 1
思路
有一个 n x n 的网格,仅由 0 和 1 组成。每次移动可以交换网格的任意两行或两列。求将网格变为棋盘的最小移动次数,如果无法变为棋盘返回 -1。所谓棋盘,指的是任意格子的值与它周围四个格子的值不同。
首先需要分析出可以转变为棋盘的条件,棋盘只有两种类型的行,它们互反,且这两种行的个数相差至多为 1。对于每种类型的行,0 的个数和 1 的个数相差至多也是 1。
然后需要求出当前行与列转化为 010101…… 或者 101010…… 所需的移动次数。求出位置不同的个数 diff,如果 n 为偶数,最小交换次数为 Math.min(diff, n - diff),如果 n 为奇数,最小交换次数为 diff/2。
代码
/**
* @date 2024-12-09 8:46
*/
public class MovesToChessboard782 {
public int movesToChessboard(int[][] board) {
int n = board.length;
int[] firstRow = board[0];
int[] firstCol = new int[n];
int[] firstRowCnt = new int[2];
int[] firstColCnt = new int[2];
for (int i = 0; i < n; i++) {
firstRowCnt[board[0][i]]++;
firstColCnt[board[i][0]]++;
firstCol[i] = board[i][0];
}
// 第一行或者第一列0与1的个数之差超过1就无法转化为棋盘。因为最终棋盘的行与列都是 101010…… 或 010101…… 的形式
if (Math.abs(firstRowCnt[0] - firstRowCnt[1]) > 1 || Math.abs(firstColCnt[0] - firstColCnt[1]) > 1) {
return -1;
}
// 判断行是否完全相同或者完全相反,这里使用异或运算来判断,如果equal == 0 说明完全相同,opposite == 0 说明完全相反,如果都不等于0说明无法转为棋盘
for (int i = 1; i < n; i++) {
int equal = 0;
int opposite = 0;
for (int j = 0; j < board[i].length; j++) {
int tmp = board[i][j] ^ board[0][j];
equal += tmp;
opposite += 1 ^ tmp;
}
if (equal != 0 && opposite != 0) {
return -1;
}
}
// 经过前面的判断,第一行与第一列的第一个格子的值一定是相同的
return minMove(firstRow, firstRowCnt) + minMove(firstCol, firstColCnt);
}
public int minMove(int[] arr, int[] cnt) {
int n = arr.length;
int start = cnt[1] > cnt[0] ? 1 : 0;
int diff = 0;
// 计算与棋盘的差异,我们移动一次可以减少两个 diff,因此最终结果需要除以2
for (int i = 0; i < n; i++) {
// i % 2 ^ start 的作用是确定 1010…… 还是 0101……,如果不考虑start 那么序列是 0101,如果需要以1开头,就需要 异或 1
diff += i % 2 ^ start ^ arr[i];
}
// 这里考虑的是 n 的奇偶性,如果n为奇数,那么必定 abs(cnt[1] - cnt[0]) == 1,多的那一个一定要放在第一个位置,移动的方案只有一种
// 如果为偶数,最终可以是 0101…… 或者 1010……,取移动次数最小的
return n % 2 != 0 ? diff / 2 : Math.min(diff, n - diff) / 2;
}
}性能