日期: 2024 年 12 月 2 日

目标

n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

示例 1：

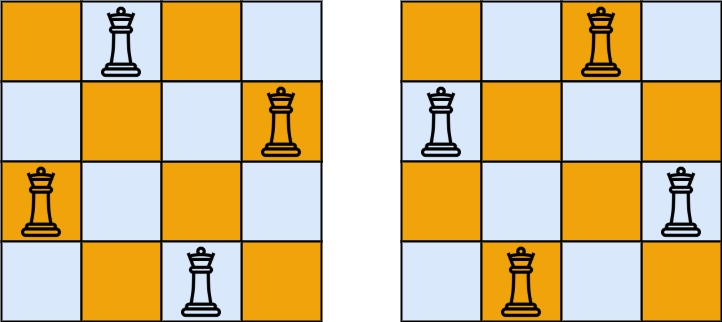
输入：n = 4
输出：2
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：1

说明：

1 <= n <= 9

思路

将 n 个皇后放在 n x n 的棋盘上，使它们不在同一行、不在同一列并且不在同一斜线上。返回不同的解决方案数量。与 51_N皇后 相比，本题无需返回具体的布局。

关键点：

• 每行只能放一个皇后，枚举当前行的每一列，如果存在合法的位置则进入下一行
• 如何判断是否在一条斜线上，对于坐标 (i, j)，(a, b)，如果 i + j == a + b || i - j == a - b，那么它们在一条斜线上
• 使用数组保存已经存在皇后的斜线，由于 i - j 可能出现负数，我们将其右移 n，使用 i - j + n，最大值为 n - 1 + n，数组初始化为 2 * n，i + j 最大值为 n - 1 + n - 1 初始化为 2 * n - 1
• 从第 0 行开始，如果能够进入第 1 行，说明第 0 行存在皇后。同理如果能够进入第 2 行，说明前两行存在皇后，总共 2 个皇后。因此结束条件为 row == n

代码

/**
 * @date 2024-12-01 17:58
 */
public class TotalNQueens52 {

    public int res;
    public int n;
    public boolean[] colIndexSet;
    public boolean[] leftDiagonalSet;
    public boolean[] rightDiagonalSet;

    public int totalNQueens(int n) {
        this.n = n;
        colIndexSet = new boolean[n];
        leftDiagonalSet = new boolean[2 * n];
        rightDiagonalSet = new boolean[2 * n - 1];
        backTracing(0);
        return res;
    }

    public void backTracing(int row) {
        if (row == n) {
            res++;
            return;
        }
        for (int col = 0; col < n; col++) {
            if (colIndexSet[col] || leftDiagonalSet[row - col + n] || rightDiagonalSet[row + col]) {
                continue;
            }
            colIndexSet[col] = true;
            leftDiagonalSet[row - col + n] = true;
            rightDiagonalSet[row + col] = true;
            backTracing(row + 1);
            colIndexSet[col] = false;
            leftDiagonalSet[row - col + n] = false;
            rightDiagonalSet[row + col] = false;
        }
    }

}

性能