目标
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
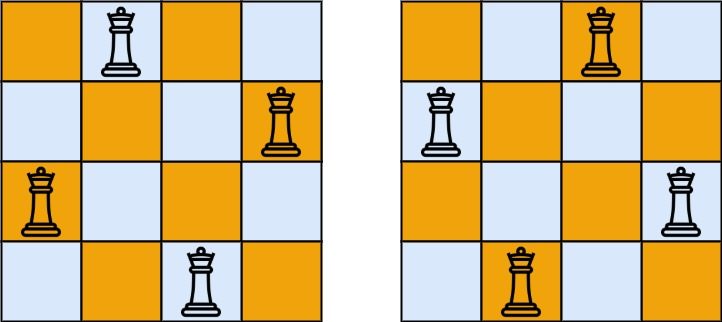
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。示例 2:
输入:n = 1
输出:[["Q"]]说明:
- 1 <= n <= 9
思路
将 n 个皇后放在 n x n 的棋盘上,使它们不在同一行、不在同一列并且不在同一斜线上。返回所有不同的解决方案,使用 Q 表示皇后,. 表示空位。
枚举棋盘的每个格子,当该格子放置皇后时,其所在行、列、斜线的格子都不能有皇后。使用回溯算法,如果格子遍历完皇后数量刚好为 n 个则计数。
假设 (i, j) 位置上放置了皇后,那么所有 (i, *) (*, j) 以及所有满足 a - b == i - j || i + j == a + b 的 (a, b) 都不能再放置皇后。
使用整数的二进制位来表示列是否允许放置皇后,从左到右对应二进制的低位到高位:
- 由于逻辑与、或没有逆运算,所以必须以参数的方式传递,否则无法恢复现场
- 如果我们在第
0行的第i列放置了皇后,那么第1行的第i - 1, i, i + 1列无法放置皇后,使用位运算的角度来看就是对 1 << i, 1 << (i + 1), 1 << (i - 1) 相与,即 1 << i, (1 << i) << 1, (1 << i) >> 1。令c = 1 << i,再考虑当前行与前面行的限制,下一行 不能放置皇后的列为:colIndexSet | c,(leftDiagonalSet | c) << 1,(rightDiagonalSet | c) >> 1),其中 colIndexSet 的 bit 1 表示无法放置皇后的列;leftDiagonalSet 的 bit 1 表示受↘斜线限制,无法放置皇后的列;rightDiagonalSet 的 bit 1 表示受↙斜线限制,无法放置皇后的列;c 表示将当前行放置皇后的列对应的 bit 位 置1所代表的数字 - valid = ((1 << n) - 1) & ~(colIndexSet | leftDiagonalSet | rightDiagonalSet) 表示合法的位置
- c = valid & -valid 得到 bit 1 的最低位表示的数字
- Integer.bitCount(c - 1) 表示列下标
- valid ^= c 将当前处理过的最低位 bit 1 置 0
当然也可以使用数组来记录不可放置皇后的列信息,差别不大,见 52_N皇后II
代码
/**
* @date 2024-12-01 16:45
*/
public class SolveNQueens51 {
public static class SolveNQueens {
public List<List<String>> res;
public int n;
public int[] queens;
public List<List<String>> solveNQueens(int n) {
this.n = n;
queens = new int[n];
res = new ArrayList<>();
backTracing(0, 0, 0, 0);
return res;
}
public void backTracing(int row, int colIndexSet, int leftDiagonalSet, int rightDiagonalSet) {
if (row == n) {
List<String> solution = new ArrayList<>(n);
char[] chars = new char[n];
Arrays.fill(chars, '.');
for (int i = 0; i < n; i++) {
chars[queens[i]] = 'Q';
solution.add(new String(chars));
chars[queens[i]] = '.';
}
res.add(solution);
return;
}
int valid = ((1 << n) - 1) & ~(colIndexSet | leftDiagonalSet | rightDiagonalSet);
while (valid > 0){
int c = valid & -valid;
queens[row] = Integer.bitCount(c - 1);
backTracing(row + 1, colIndexSet | c,
(leftDiagonalSet | c) << 1,
(rightDiagonalSet | c) >> 1);
valid ^= c;
}
}
}
public List<List<String>> res;
public Set<Integer> rowIndexSet;
public Set<Integer> colIndexSet;
public Set<Integer> leftDiagonalSet;
public Set<Integer> rightDiagonalSet;
public ArrayList<int[]> indexList;
public int end;
public int n;
public List<List<String>> solveNQueens(int n) {
res = new ArrayList<>(n);
rowIndexSet = new HashSet<>(n);
colIndexSet = new HashSet<>(n);
leftDiagonalSet = new HashSet<>(n);
rightDiagonalSet = new HashSet<>(n);
indexList = new ArrayList<>(n);
end = n * n;
this.n = n;
for (int i = 0; i < n; i++) {
backTracing(i);
}
return res;
}
public void backTracing(int index) {
int row = index / n;
int col = index % n;
int leftDiagonal = row - col;
int rightDiagonal = row + col;
rowIndexSet.add(row);
colIndexSet.add(col);
leftDiagonalSet.add(leftDiagonal);
rightDiagonalSet.add(rightDiagonal);
indexList.add(new int[]{row, col});
if (indexList.size() == n) {
StringBuilder sb = new StringBuilder();
List<String> solution = new ArrayList<>(n);
for (int[] cor : indexList) {
for (int i = 0; i < n; i++) {
if (i == cor[1]) {
sb.append('Q');
} else {
sb.append('.');
}
}
solution.add(sb.toString());
sb.setLength(0);
}
res.add(solution);
}
for (int i = index + 1; i < end; i++) {
int r = i / n;
int c = i % n;
int ld = r - c;
int rd = r + c;
if (rowIndexSet.contains(r) || colIndexSet.contains(c)
|| leftDiagonalSet.contains(ld)
|| rightDiagonalSet.contains(rd)) {
continue;
}
backTracing(i);
}
rowIndexSet.remove(row);
colIndexSet.remove(col);
leftDiagonalSet.remove(leftDiagonal);
rightDiagonalSet.remove(rightDiagonal);
indexList.remove(indexList.size() - 1);
}
}
性能