月度归档: 2024 年 12 月
3219.切蛋糕的最小总开销II
目标
有一个 m x n 大小的矩形蛋糕,需要切成 1 x 1 的小块。
给你整数 m ,n 和两个数组:
- horizontalCut 的大小为 m - 1 ,其中 horizontalCut[i] 表示沿着水平线 i 切蛋糕的开销。
- verticalCut 的大小为 n - 1 ,其中 verticalCut[j] 表示沿着垂直线 j 切蛋糕的开销。
一次操作中,你可以选择任意不是 1 x 1 大小的矩形蛋糕并执行以下操作之一:
- 沿着水平线 i 切开蛋糕,开销为 horizontalCut[i] 。
- 沿着垂直线 j 切开蛋糕,开销为 verticalCut[j] 。
每次操作后,这块蛋糕都被切成两个独立的小蛋糕。
每次操作的开销都为最开始对应切割线的开销,并且不会改变。
请你返回将蛋糕全部切成 1 x 1 的蛋糕块的 最小 总开销。
示例 1:
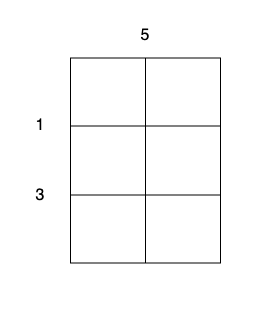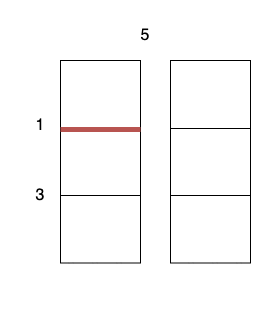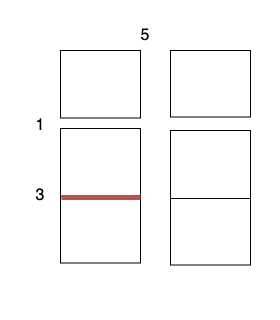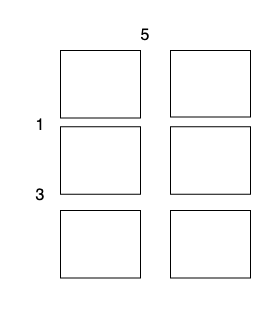
输入:m = 3, n = 2, horizontalCut = [1,3], verticalCut = [5]
输出:13
解释:
沿着垂直线 0 切开蛋糕,开销为 5 。
沿着水平线 0 切开 3 x 1 的蛋糕块,开销为 1 。
沿着水平线 0 切开 3 x 1 的蛋糕块,开销为 1 。
沿着水平线 1 切开 2 x 1 的蛋糕块,开销为 3 。
沿着水平线 1 切开 2 x 1 的蛋糕块,开销为 3 。
总开销为 5 + 1 + 1 + 3 + 3 = 13 。示例 2:
输入:m = 2, n = 2, horizontalCut = [7], verticalCut = [4]
输出:15
解释:
沿着水平线 0 切开蛋糕,开销为 7 。
沿着垂直线 0 切开 1 x 2 的蛋糕块,开销为 4 。
沿着垂直线 0 切开 1 x 2 的蛋糕块,开销为 4 。
总开销为 7 + 4 + 4 = 15 。说明:
- 1 <= m, n <= 10^5
- horizontalCut.length == m - 1
- verticalCut.length == n - 1
- 1 <= horizontalCut[i], verticalCut[i] <= 10^3
思路
有一块 m x n 的蛋糕,horizontalCut[i] 表示水平切第 i 行的开销,verticalCut[i] 表示垂直切第 i 列的开销。求将蛋糕切成 1 x 1 小块的最小代价。
与 切蛋糕的最小总开销I 相比数据范围扩大了,返回值是 long 型。
代码
/**
* @date 2024-12-26 16:38
*/
public class MinimumCost3219 {
public long minimumCost(int m, int n, int[] horizontalCut, int[] verticalCut) {
int horizontalPart = m;
int verticalPart = n;
Arrays.sort(horizontalCut);
Arrays.sort(verticalCut);
int h = 0;
int v = 0;
long res = 0;
while (h < m - 1 || v < n - 1) {
int hcost = h >= m - 1 ? Integer.MAX_VALUE : horizontalCut[h];
int vcost = v >= n - 1 ? Integer.MAX_VALUE : verticalCut[v];
if (hcost < vcost) {
res += verticalPart * hcost;
horizontalPart--;
h++;
} else {
res += horizontalPart * vcost;
verticalPart--;
v++;
}
}
return res;
}
}
性能
1367.二叉树中的链表
目标
给你一棵以 root 为根的二叉树和一个 head 为第一个节点的链表。
如果在二叉树中,存在一条一直向下的路径,且每个点的数值恰好一一对应以 head 为首的链表中每个节点的值,那么请你返回 True ,否则返回 False 。
一直向下的路径的意思是:从树中某个节点开始,一直连续向下的路径。
示例 1:
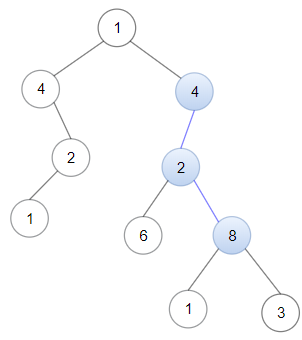
输入:head = [4,2,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
输出:true
解释:树中蓝色的节点构成了与链表对应的子路径。示例 2:
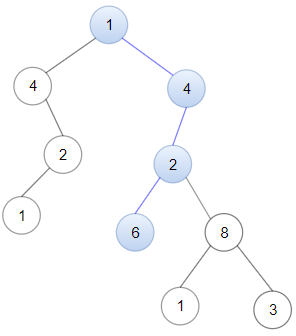
输入:head = [1,4,2,6], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
输出:true示例 3:
输入:head = [1,4,2,6,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
输出:false
解释:二叉树中不存在一一对应链表的路径。说明:
- 二叉树和链表中的每个节点的值都满足 1 <= node.val <= 100 。
- 链表包含的节点数目在 1 到 100 之间。
- 二叉树包含的节点数目在 1 到 2500 之间。
思路
判断二叉树中是否存在给定的路径 head,路径以链表的形式给出。
dfs 判断是否存在相同的路径。这道题的难点在于没有要求起点为 root,因此需要枚举所有节点为起点的情况。针对每一个起点我们最多检查 100 次,总共大概 2.5 * 10^5 次。
代码
/**
* @date 2024-12-30 8:56
*/
public class IsSubPath1367 {
public ListNode head;
public boolean isSubPath(ListNode head, TreeNode root) {
this.head = head;
return dfs(root, head);
}
public boolean dfs(TreeNode cur, ListNode node) {
if (node == null) {
return true;
}
if (cur == null) {
return false;
}
return cur.val == node.val && (dfs(cur.left, node.next) || dfs(cur.right, node.next))
|| node == head && (dfs(cur.left, head) || dfs(cur.right, head));
}
}
性能
1366.通过投票对团队排名
目标
现在有一个特殊的排名系统,依据参赛团队在投票人心中的次序进行排名,每个投票者都需要按从高到低的顺序对参与排名的所有团队进行排位。
排名规则如下:
- 参赛团队的排名次序依照其所获「排位第一」的票的多少决定。如果存在多个团队并列的情况,将继续考虑其「排位第二」的票的数量。以此类推,直到不再存在并列的情况。
- 如果在考虑完所有投票情况后仍然出现并列现象,则根据团队字母的字母顺序进行排名。
给你一个字符串数组 votes 代表全体投票者给出的排位情况,请你根据上述排名规则对所有参赛团队进行排名。
请你返回能表示按排名系统 排序后 的所有团队排名的字符串。
示例 1:
输入:votes = ["ABC","ACB","ABC","ACB","ACB"]
输出:"ACB"
解释:
A 队获得五票「排位第一」,没有其他队获得「排位第一」,所以 A 队排名第一。
B 队获得两票「排位第二」,三票「排位第三」。
C 队获得三票「排位第二」,两票「排位第三」。
由于 C 队「排位第二」的票数较多,所以 C 队排第二,B 队排第三。示例 2:
输入:votes = ["WXYZ","XYZW"]
输出:"XWYZ"
解释:
X 队在并列僵局打破后成为排名第一的团队。X 队和 W 队的「排位第一」票数一样,但是 X 队有一票「排位第二」,而 W 没有获得「排位第二」。示例 3:
输入:votes = ["ZMNAGUEDSJYLBOPHRQICWFXTVK"]
输出:"ZMNAGUEDSJYLBOPHRQICWFXTVK"
解释:只有一个投票者,所以排名完全按照他的意愿。说明:
- 1 <= votes.length <= 1000
- 1 <= votes[i].length <= 26
- votes[i].length == votes[j].length for 0 <= i, j < votes.length
votes[i][j]是英文 大写 字母- votes[i] 中的所有字母都是唯一的
- votes[0] 中出现的所有字母 同样也 出现在 votes[j] 中,其中 1 <= j < votes.length
思路
投票人对所有团队的排名用一个字符串 votes[i] 表示,团队的先后顺序就代表排名。根据所有投票人的排名对团队排名,排名第一次数最多的为第一名,如果相同则根据排名第二的次数排名,以此类推,如果最终都相同,则以团队名在字母表的先后顺序排名。
考虑自定义数据结构,维护团队在每一个名次的得票数,然后使用优先队列自定义排序。
代码
/**
* @date 2024-12-29 18:36
*/
public class RankTeams1366 {
public static class Rank {
public int name;
public int[] cnt;
public Rank(int name, int[] cnt) {
this.name = name;
this.cnt = cnt;
}
}
public String rankTeams(String[] votes) {
int n = votes[0].length();
PriorityQueue<Rank> q = new PriorityQueue<>((a, b) -> {
int[] cnta = a.cnt;
int[] cntb = b.cnt;
int i = 0;
while (i < n && cnta[i] == cntb[i]) {
i++;
}
if (i == n) {
return a.name - b.name;
}
return cntb[i] - cnta[i];
});
int[][] cnt = new int[26][n];
for (String vote : votes) {
for (int i = 0; i < vote.length(); i++) {
int c = vote.charAt(i) - 'A';
cnt[c][i]++;
}
}
for (int i = 0; i < 26; i++) {
q.offer(new Rank(i, cnt[i]));
}
char[] chars = new char[n];
int i = 0;
while (i < n) {
chars[i++] = (char) (q.poll().name + (int) 'A');
}
return new String(chars);
}
}
性能
3046.分割数组
目标
给你一个长度为 偶数 的整数数组 nums 。你需要将这个数组分割成 nums1 和 nums2 两部分,要求:
- nums1.length == nums2.length == nums.length / 2 。
- nums1 应包含 互不相同 的元素。
- nums2也应包含 互不相同 的元素。
如果能够分割数组就返回 true ,否则返回 false 。
示例 1:
输入:nums = [1,1,2,2,3,4]
输出:true
解释:分割 nums 的可行方案之一是 nums1 = [1,2,3] 和 nums2 = [1,2,4] 。示例 2:
输入:nums = [1,1,1,1]
输出:false
解释:分割 nums 的唯一可行方案是 nums1 = [1,1] 和 nums2 = [1,1] 。但 nums1 和 nums2 都不是由互不相同的元素构成。因此,返回 false 。说明:
- 1 <= nums.length <= 100
- nums.length % 2 == 0
- 1 <= nums[i] <= 100
思路
判断数组中同一元素的出现次数不超过两次。
代码
/**
* @date 2024-12-28 19:16
*/
public class IsPossibleToSplit3046 {
public boolean isPossibleToSplit(int[] nums) {
int[] cnt = new int[101];
for (int num : nums) {
if (++cnt[num] > 2) {
return false;
}
}
return true;
}
}
性能

3159.查询数组中元素的出现位置
目标
给你一个整数数组 nums ,一个整数数组 queries 和一个整数 x 。
对于每个查询 queries[i] ,你需要找到 nums 中第 queries[i] 个 x 的位置,并返回它的下标。如果数组中 x 的出现次数少于 queries[i] ,该查询的答案为 -1 。
请你返回一个整数数组 answer ,包含所有查询的答案。
示例 1:
输入:nums = [1,3,1,7], queries = [1,3,2,4], x = 1
输出:[0,-1,2,-1]
解释:
第 1 个查询,第一个 1 出现在下标 0 处。
第 2 个查询,nums 中只有两个 1 ,所以答案为 -1 。
第 3 个查询,第二个 1 出现在下标 2 处。
第 4 个查询,nums 中只有两个 1 ,所以答案为 -1 。示例 2:
输入:nums = [1,2,3], queries = [10], x = 5
输出:[-1]
解释:
第 1 个查询,nums 中没有 5 ,所以答案为 -1 。说明:
- 1 <= nums.length, queries.length <= 10^5
- 1 <= queries[i] <= 10^5
- 1 <= nums[i], x <= 10^4
思路
查询给定数字 x 在数组 nums 中第 queries[i] 次出现的下标。
一次遍历记录所有 x 的下标即可。
代码
/**
* @date 2024-12-27 6:40
*/
public class OccurrencesOfElement3159 {
public int[] occurrencesOfElement_v1(int[] nums, int[] queries, int x) {
int n = nums.length;
int max = 0;
for (int i = 0; i < n; i++) {
if (nums[i] == x) {
nums[max++] = i;
}
}
int length = queries.length;
for (int i = 0; i < length; i++) {
queries[i] = queries[i] > max ? -1 : nums[queries[i] - 1];
}
return queries;
}
}
性能

3083.字符串及其反转中是否存在同一子字符串
目标
给你一个字符串 s ,请你判断字符串 s 是否存在一个长度为 2 的子字符串,在其反转后的字符串中也出现。
如果存在这样的子字符串,返回 true;如果不存在,返回 false 。
示例 1:
输入:s = "leetcode"
输出:true
解释:子字符串 "ee" 的长度为 2,它也出现在 reverse(s) == "edocteel" 中。示例 2:
输入:s = "abcba"
输出:true
解释:所有长度为 2 的子字符串 "ab"、"bc"、"cb"、"ba" 也都出现在 reverse(s) == "abcba" 中。示例 3:
输入:s = "abcd"
输出:false
解释:字符串 s 中不存在满足「在其反转后的字符串中也出现」且长度为 2 的子字符串。说明:
- 1 <= s.length <= 100
- 字符串 s 仅由小写英文字母组成。
思路
判断字符串 s 中长度为 2 的子串是否在其反转后的字符串中出现,返回 true 或 false。
直接的想法是将 s 中所有长度为 2 的子串放入 hashset,然后判断倒序字符串的长度为 2 的子串是否在集合中。
网友题解使用 int[] 记录所有出现过的长度为 2 的子串,下标表示第一个字母,第二个字母则使用 int 值的 bit 位表示。
代码
/**
* @date 2024-12-26 8:47
*/
public class IsSubstringPresent3083 {
public boolean isSubstringPresent(String s) {
int n = s.length();
int[] exists = new int[26];
for (int i = 0; i < n - 1; i++) {
int a = s.charAt(i) - 'a';
int b = s.charAt(i + 1) - 'a';
exists[a] |= 1 << b;
if ((exists[b] >> a & 1) == 1) {
return true;
}
}
return false;
}
}
性能
3218.切蛋糕的最小总开销 I
目标
有一个 m x n 大小的矩形蛋糕,需要切成 1 x 1 的小块。
给你整数 m ,n 和两个数组:
- horizontalCut 的大小为 m - 1 ,其中 horizontalCut[i] 表示沿着水平线 i 切蛋糕的开销。
- verticalCut 的大小为 n - 1 ,其中 verticalCut[j] 表示沿着垂直线 j 切蛋糕的开销。
一次操作中,你可以选择任意不是 1 x 1 大小的矩形蛋糕并执行以下操作之一:
- 沿着水平线 i 切开蛋糕,开销为 horizontalCut[i] 。
- 沿着垂直线 j 切开蛋糕,开销为 verticalCut[j] 。
每次操作后,这块蛋糕都被切成两个独立的小蛋糕。
每次操作的开销都为最开始对应切割线的开销,并且不会改变。
请你返回将蛋糕全部切成 1 x 1 的蛋糕块的 最小 总开销。
示例 1:
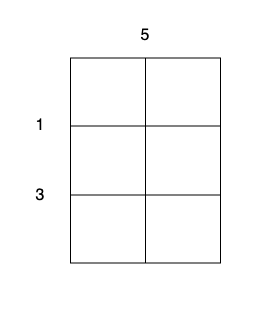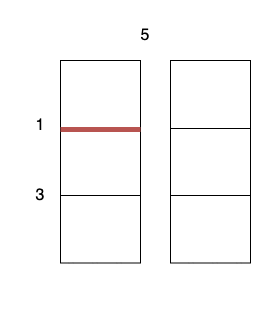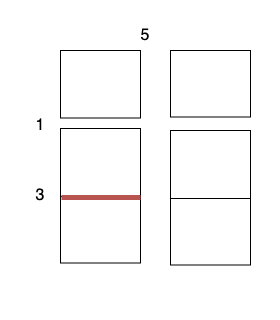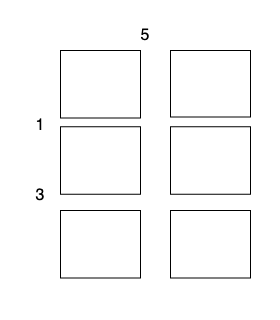
输入:m = 3, n = 2, horizontalCut = [1,3], verticalCut = [5]
输出:13
解释:
沿着垂直线 0 切开蛋糕,开销为 5 。
沿着水平线 0 切开 3 x 1 的蛋糕块,开销为 1 。
沿着水平线 0 切开 3 x 1 的蛋糕块,开销为 1 。
沿着水平线 1 切开 2 x 1 的蛋糕块,开销为 3 。
沿着水平线 1 切开 2 x 1 的蛋糕块,开销为 3 。
总开销为 5 + 1 + 1 + 3 + 3 = 13 。示例 2:
输入:m = 2, n = 2, horizontalCut = [7], verticalCut = [4]
输出:15
解释:
沿着水平线 0 切开蛋糕,开销为 7 。
沿着垂直线 0 切开 1 x 2 的蛋糕块,开销为 4 。
沿着垂直线 0 切开 1 x 2 的蛋糕块,开销为 4 。
总开销为 7 + 4 + 4 = 15 。说明:
- 1 <= m, n <= 20
- horizontalCut.length == m - 1
- verticalCut.length == n - 1
- 1 <= horizontalCut[i], verticalCut[i] <= 10^3
思路
有一块 m x n 的蛋糕,horizontalCut[i] 表示水平切第 i 行的开销,verticalCut[i] 表示垂直切第 i 列的开销。求将蛋糕切成 1 x 1 小块的最小代价。
需要注意每次切的蛋糕必须是整块的,并不能将几块蛋糕排到一起切。
我们应该先沿着代价最大的位置切吗?比如大小为 2 x 100 的蛋糕,水平切的代价为 99,垂直切每一列的代价为 100。先切每一列代价为 99 * 100,然后对切开的 100 块水平切 100 次,代价为 100 * 99,总代价为 2 * 99 * 100。如果先水平切一次,代价为 99。然后需要垂直切 2 * 99 次,代价为 2 * 99 * 100,总代价为 99 + 2 * 99 * 100。这种贪心策略应该是可行的,因为每切一次块数会增加,现在不切代价大的,后面再切的时候代价会增加。
选择沿某一水平或垂直线切割时,需要记录水平 和 垂直方向蛋糕块的数量,用来计算代价。每切一次,横向与纵向的蛋糕块就会增加一个。
刚开始不确定能否使用贪心策略,考虑如何表示哪些切过了,哪些没切,卡了很久。关键点是如何将问题抽象建模,使用分治思想,不要面向过程。每切一次之后,问题转化为切剩余蛋糕的子问题。我们可以使用记忆化搜索解空间,求出最小值。
代码
/**
* @date 2024-12-25 10:41
*/
public class MinimumCost3218 {
public int minimumCost_v1(int m, int n, int[] horizontalCut, int[] verticalCut) {
int horizontalCutPart = 1;
int verticalCutPart = 1;
Arrays.sort(horizontalCut);
Arrays.sort(verticalCut);
int h = horizontalCut.length - 1;
int v = verticalCut.length - 1;
int res = 0;
while (h >= 0 || v >= 0) {
if (h < 0){
res += horizontalCutPart * verticalCut[v];
v--;
continue;
}
if (v < 0){
res += verticalCutPart * horizontalCut[h];
h--;
continue;
}
if (horizontalCut[h] > verticalCut[v]) {
res += verticalCutPart * horizontalCut[h];
horizontalCutPart++;
h--;
} else if (horizontalCut[h] <= verticalCut[v]) {
res += horizontalCutPart * verticalCut[v];
verticalCutPart++;
v--;
}
}
return res;
}
int[] rowCost;
int[] colCost;
int[][][][] mem;
public int minimumCost(int m, int n, int[] horizontalCut, int[] verticalCut) {
this.rowCost = horizontalCut;
this.colCost = verticalCut;
mem = new int[m + 1][m + 1][n + 1][n + 1];
// rowStart rowEnd colStart colEnd 表示蛋糕的边界
// 0 1 2 3 4 5 ... n
// 0 ———————————————————
// | | | | | |
// 1 ———————————————————
// | | | | | |
// 2 ———————————————————
// | | | | | |
// 3 ———————————————————
// | | | | | |
// 4 ———————————————————
// | | | | | |
// 5 ———————————————————
// ...
// m
return dfs(0, m, 0, n);
}
public int dfs(int rowStart, int rowEnd, int colStart, int colEnd) {
if (rowEnd - rowStart == 1 && colEnd - colStart == 1) {
return 0;
}
int res = Integer.MAX_VALUE;
for (int i = rowStart + 1; i < rowEnd; i++) {
if (mem[rowStart][i][colStart][colEnd] == 0) {
mem[rowStart][i][colStart][colEnd] = dfs(rowStart, i, colStart, colEnd);
}
if (mem[i][rowEnd][colStart][colEnd] == 0) {
mem[i][rowEnd][colStart][colEnd] = dfs(i, rowEnd, colStart, colEnd);
}
res = Math.min(res, rowCost[i - 1] + mem[rowStart][i][colStart][colEnd] + mem[i][rowEnd][colStart][colEnd]);
}
for (int i = colStart + 1; i < colEnd; i++) {
if (mem[rowStart][rowEnd][colStart][i] == 0) {
mem[rowStart][rowEnd][colStart][i] = dfs(rowStart, rowEnd, colStart, i);
}
if (mem[rowStart][rowEnd][i][colEnd] == 0) {
mem[rowStart][rowEnd][i][colEnd] = dfs(rowStart, rowEnd, i, colEnd);
}
res = Math.min(res, colCost[i - 1] + mem[rowStart][rowEnd][colStart][i] + mem[rowStart][rowEnd][i][colEnd]);
}
return res;
}
}
性能

1705.吃苹果的最大数目
目标
有一棵特殊的苹果树,一连 n 天,每天都可以长出若干个苹果。在第 i 天,树上会长出 apples[i] 个苹果,这些苹果将会在 days[i] 天后(也就是说,第 i + days[i] 天时)腐烂,变得无法食用。也可能有那么几天,树上不会长出新的苹果,此时用 apples[i] == 0 且 days[i] == 0 表示。
你打算每天 最多 吃一个苹果来保证营养均衡。注意,你可以在这 n 天之后继续吃苹果。
给你两个长度为 n 的整数数组 days 和 apples ,返回你可以吃掉的苹果的最大数目。
示例 1:
输入:apples = [1,2,3,5,2], days = [3,2,1,4,2]
输出:7
解释:你可以吃掉 7 个苹果:
- 第一天,你吃掉第一天长出来的苹果。
- 第二天,你吃掉一个第二天长出来的苹果。
- 第三天,你吃掉一个第二天长出来的苹果。过了这一天,第三天长出来的苹果就已经腐烂了。
- 第四天到第七天,你吃的都是第四天长出来的苹果。示例 2:
输入:apples = [3,0,0,0,0,2], days = [3,0,0,0,0,2]
输出:5
解释:你可以吃掉 5 个苹果:
- 第一天到第三天,你吃的都是第一天长出来的苹果。
- 第四天和第五天不吃苹果。
- 第六天和第七天,你吃的都是第六天长出来的苹果。说明:
- apples.length == n
- days.length == n
- 1 <= n <= 2 * 10^4
- 0 <= apples[i], days[i] <= 2 * 10^4
- 只有在 apples[i] = 0 时,days[i] = 0 才成立
思路
有一颗特殊的苹果树,第 i 天会结出 apples[i] 个果子,这些果子将在第 i + days[i] 天腐烂。求每天吃一个未腐烂的苹果,最多可以吃几个。
我们的贪心策略是优先吃快腐烂的苹果,首先将当天结果的苹果个数以及腐烂时间放入最小堆,获取堆顶最近要腐烂的苹果,判断是否已经腐烂,如果没有将苹果个数减一,如果数量减为 0 或者已经腐烂,将其从堆中移出。
代码
/**
* @date 2024-12-24 10:35
*/
public class EatenApples1705 {
public int eatenApples_v2(int[] apples, int[] days) {
int n = apples.length;
PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> a[1] - b[1]);
int res = 0;
for (int day = 0; day < n || !q.isEmpty(); day++) {
if (day < n && apples[day] > 0){
q.offer(new int[]{apples[day], day + days[day]});
}
while (!q.isEmpty()) {
int[] applesInfo = q.peek();
if (applesInfo[0] == 0 || applesInfo[1] == day) {
q.poll();
continue;
}
if (applesInfo[1] > day && applesInfo[0] > 0) {
applesInfo[0]--;
res++;
break;
}
}
}
return res;
}
}
性能
855.考场就座
目标
在考场里,一排有 N 个座位,分别编号为 0, 1, 2, ..., N-1 。
当学生进入考场后,他必须坐在能够使他与离他最近的人之间的距离达到最大化的座位上。如果有多个这样的座位,他会坐在编号最小的座位上。(另外,如果考场里没有人,那么学生就坐在 0 号座位上。)
返回 ExamRoom(int N) 类,它有两个公开的函数:其中,函数 ExamRoom.seat() 会返回一个 int (整型数据),代表学生坐的位置;函数 ExamRoom.leave(int p) 代表坐在座位 p 上的学生现在离开了考场。每次调用 ExamRoom.leave(p) 时都保证有学生坐在座位 p 上。
示例:
输入:["ExamRoom","seat","seat","seat","seat","leave","seat"], [[10],[],[],[],[],[4],[]]
输出:[null,0,9,4,2,null,5]
解释:
ExamRoom(10) -> null
seat() -> 0,没有人在考场里,那么学生坐在 0 号座位上。
seat() -> 9,学生最后坐在 9 号座位上。
seat() -> 4,学生最后坐在 4 号座位上。
seat() -> 2,学生最后坐在 2 号座位上。
leave(4) -> null
seat() -> 5,学生最后坐在 5 号座位上。说明:
- 1 <= N <= 10^9
- 在所有的测试样例中 ExamRoom.seat() 和 ExamRoom.leave() 最多被调用 10^4 次。
- 保证在调用 ExamRoom.leave(p) 时有学生正坐在座位 p 上。
思路
有一排座位编号为 0 ~ N - 1,当学生进入考场后可以选择距离其它同学最远的位置坐下。实现 ExamRoom 类,提供 seat() 方法返回合法的座位,以及 leave() 方法允许学生离开考场。
显然下一个进入考场的同学应该坐在当前相邻座位最大距离的中间位置,考虑到允许离开座位,那么端点的座位离开的情况也要考虑。我们需要提供一个类,快速地查询相邻学生座位的最大值,并且支持座位的删减。
使用最大堆,堆中元素为 [距离左边相邻同学的距离,座位编号],根据 距离/2 排序,除以 2 是为了消除左右距离不等造成的影响。例如 0 4 9 这种情况,区间长度一个是 4,一个是 5,但是 2 ~ 4,4 ~ 6 的距离相同,应该取编号最小的。
计算下一个座位时,需要考虑三种情况:
- 如果是第一个同学进入考场,直接坐在 0 号位置
- 如果只有一个同学在考场,下一个同学需要坐在距离该位置距离最大的端点
- 如果有大于两个同学在考场,我们可以选择两个同学中间的位置,或者两端的位置
如何处理离开考场的情况?如果离开的同学左右位置有人,需要进行区间合并,将合并后的区间放入堆中,并且删除堆中左右两侧区间。但是在堆中查找元素的时间复杂度是 O(n),由于最多总共调用 10^4 次,leave 最多调用 k = 5 * 10^3 次,堆中元素个数随着调用减少,总复杂度为 O(k^2) 可能勉强通过。
为了快速访问左右的相邻座位以便区间合并以及左右端点的距离判断,使用 TreeSet 记录同学的座位编号。我们可以将删除操作延迟到获取座位的时候处理。
代码
/**
* @date 2024-12-23 14:28
*/
public class ExamRoom {
private TreeSet<Integer> occupied;
// [distance, no]
private PriorityQueue<int[]> q;
private int n;
public ExamRoom(int n) {
this.n = n;
occupied = new TreeSet<>();
q = new PriorityQueue<>((a, b) -> {
int compare = b[0] / 2 - a[0] / 2;
if (compare != 0) {
return compare;
}
return a[1] - b[1];
});
}
public int seat() {
if (occupied.size() == 0) {
occupied.add(0);
return 0;
} else if (occupied.size() == 1) {
Integer no = occupied.first();
int distance = n - 1 - no;
if (distance > no) {
q.offer(new int[]{distance, n - 1});
occupied.add(n - 1);
return n - 1;
} else {
q.offer(new int[]{no, no});
occupied.add(0);
return 0;
}
} else {
while (true) {
int first = occupied.first();
int last = occupied.last();
int rd = n - 1 - last;
int[] dn = q.peek();
int r = dn[1];
int l = r - dn[0];
// 注意第三个条件,可以防止离开座位后又有同学坐下,由于延迟删除,距离并未更新导致的计算错误
if (!occupied.contains(l) || !occupied.contains(r) || occupied.higher(l) != r) {
q.poll();
continue;
}
int distance = dn[0] / 2;
if (distance <= first || distance < rd) {
if (first < rd) {
q.offer(new int[]{rd, n - 1});
occupied.add(n - 1);
return n - 1;
} else {
q.offer(new int[]{l, l});
occupied.add(0);
return 0;
}
} else {
q.poll();
int m = l + (r - l) / 2;
occupied.add(m);
q.offer(new int[]{m - l, m});
q.offer(new int[]{r - m, r});
return m;
}
}
}
}
public void leave(int p) {
if (p != occupied.first() && p != occupied.last()) {
int l = occupied.lower(p);
int r = occupied.higher(p);
q.offer(new int[]{r - l, r});
}
occupied.remove(p);
}
}
性能