目标
给你一个整数数组 colors 和一个整数 k ,colors表示一个由红色和蓝色瓷砖组成的环,第 i 块瓷砖的颜色为 colors[i] :
- colors[i] == 0 表示第 i 块瓷砖的颜色是 红色 。
- colors[i] == 1 表示第 i 块瓷砖的颜色是 蓝色 。
环中连续 k 块瓷砖的颜色如果是 交替 颜色(也就是说除了第一块和最后一块瓷砖以外,中间瓷砖的颜色与它 左边 和 右边 的颜色都不同),那么它被称为一个 交替 组。
请你返回 交替 组的数目。
注意 ,由于 colors 表示一个 环 ,第一块 瓷砖和 最后一块 瓷砖是相邻的。
示例 1:
输入:colors = [0,1,0,1,0], k = 3
输出:3解释:
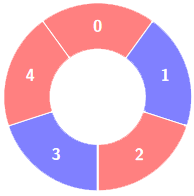
交替组包括:
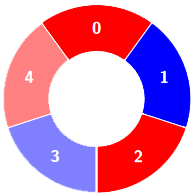
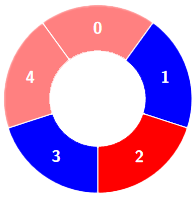
示例 2:
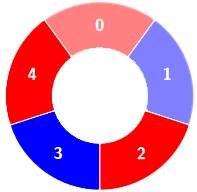
输入:colors = [0,1,0,0,1,0,1], k = 6
输出:2解释:

交替组包括:


示例 3:
输入:colors = [1,1,0,1], k = 4
输出:0解释:
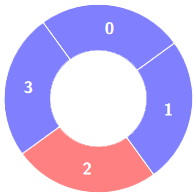
说明:
- 3 <= colors.length <= 10^5
- 0 <= colors[i] <= 1
- 3 <= k <= colors.length
思路
有一个环形二进制数组(认为首尾相邻),如果连续的 k 个元素除了第一个与最后一个元素外,内部元素与它左边和右边的元素不同,则称这 k 个元素为一个交替组,求交替组的个数。
如果 k 取 3 就变成了 3206.交替组I。
昨天的题枚举的是中间元素,今天这道题我们可以枚举左端点。将其视为一个特殊的滑动窗口问题,特殊之处在于窗口内元素需要满足的条件是 不存在连续相等的元素。显然,如果新移入窗口的元素使得条件不满足,即窗口内后两个元素相等,那么只要窗口内包含这个新移入的元素 条件就总是无法满足。
因此可以直接将左端点移到右边界,省去了移出元素的滑动过程。在向右扩展的时候可以对窗口内的元素计数,如果大于等于 k 则计入结果,直到右端点无法再继续扩展,重置计数器,然后以右边界为左端点继续该过程。
可以省略维护左边界的指针,重置计数器就相当于从当前位置重新计数。
我们可以通过偏移下标然后取余来处理环形数组的遍历。也可以参考 134.加油站 两次循环。
代码
/**
* @date 2024-11-26 9:31
*/
public class NumberOfAlternatingGroups3208 {
/**
* 两次循环1ms
*/
public int numberOfAlternatingGroups_v2(int[] colors, int k) {
int res = 0;
int n = colors.length;
int prev = colors[n - k + 1];
int size = 1;
for (int i = n - k + 2; i < n; i++) {
if (colors[i] == prev) {
size = 1;
} else {
size++;
}
prev = colors[i];
}
for (int i = 0; i < n; i++) {
if (colors[i] == prev) {
size = 1;
} else {
size++;
}
prev = colors[i];
if (size >= k) {
res++;
}
}
return res;
}
/**
* 5ms
*/
public int numberOfAlternatingGroups_v1(int[] colors, int k) {
int res = 0;
int n = colors.length;
int size = 1;
for (int i = n - k + 2; i < 2 * n; i++) {
if (colors[i % n] == colors[(i - 1) % n]) {
size = 1;
} else {
size++;
}
if (size >= k) {
res++;
}
}
return res;
}
}
性能