日期: 2024 年 11 月 26 日

目标

给你一个整数数组 colors ，它表示一个由红色和蓝色瓷砖组成的环，第 i 块瓷砖的颜色为 colors[i] ：

• colors[i] == 0 表示第 i 块瓷砖的颜色是 红色 。
• colors[i] == 1 表示第 i 块瓷砖的颜色是 蓝色 。

环中连续 3 块瓷砖的颜色如果是 交替 颜色（也就是说中间瓷砖的颜色与它 左边 和 右边 的颜色都不同），那么它被称为一个 交替 组。

请你返回 交替 组的数目。

注意 ，由于 colors 表示一个 环 ，第一块 瓷砖和 最后一块 瓷砖是相邻的。

示例 1：

输入：colors = [1,1,1]
输出：0

解释：

示例 2：

输入：colors = [0,1,0,0,1]
输出：3

解释：

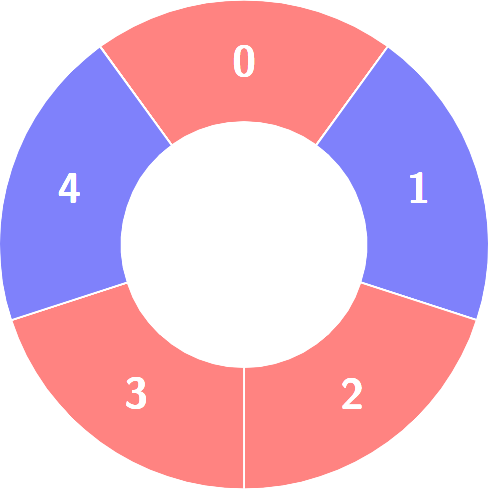
交替组包括：

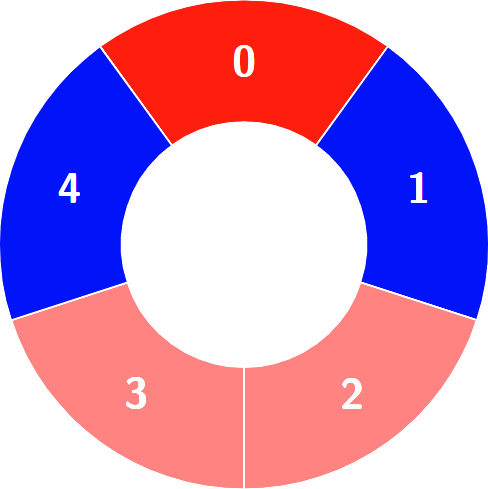
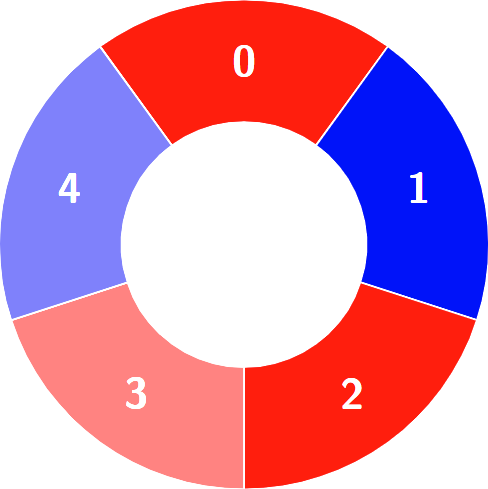
说明：

• 3 <= colors.length <= 100
• 0 <= colors[i] <= 1

思路

有一个环形二进制数组（认为首尾相邻），判断存在多少个交替组，如果元素与它左右相邻的两个元素值不相等，称这三个元素为一个交替组。

直接模拟判断即可，第一个元素的左邻居以及最后一个元素的右邻居需要特殊处理。也可以通过取模统一处理，定义 i 的初值为 n，i < 2n，循环内下标使用 (i - 1) % n，i % n，(i + 1) % n，不过没有必要对循环内的所有下标进行模运算，特殊处理效率更高。

官网题解循环使用的初值是 0，i < n，不过循环内部计算的是 (i - 1 + n) % n，i，(i + 1) % n，节省了两次 i % n 取余运算。

代码

/**
 * @date 2024-11-26 8:56
 */
public class NumberOfAlternatingGroups3206 {

    public int numberOfAlternatingGroups_v1(int[] colors) {
        int n = colors.length;
        int res = 0;
        boolean b = colors[n - 1] != colors[0];
        if (colors[0] != colors[1] && b) {
            res++;
        }
        if (colors[n - 1] != colors[n - 2] && b) {
            res++;
        }
        for (int i = 1; i < n - 1; i++) {
            if (colors[i - 1] != colors[i] && colors[i + 1] != colors[i]) {
                res++;
            }
        }
        return res;
    }

    public int numberOfAlternatingGroups(int[] colors) {
        int n = colors.length;
        int res = 0;
        for (int i = n; i < 2 * n; i++) {
            if (colors[(i - 1) % n] != colors[i % n] && colors[(i + 1) % n] != colors[i % n]) {
                res++;
            }
        }
        return res;
    }
}

性能