目标
给你一个整数 n 和一个二维整数数组 queries。
有 n 个城市,编号从 0 到 n - 1。初始时,每个城市 i 都有一条单向道路通往城市 i + 1( 0 <= i < n - 1)。
queries[i] = [ui, vi] 表示新建一条从城市 ui 到城市 vi 的单向道路。每次查询后,你需要找到从城市 0 到城市 n - 1 的最短路径的长度。
所有查询中不会存在两个查询都满足 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。
返回一个数组 answer,对于范围 [0, queries.length - 1] 中的每个 i,answer[i] 是处理完前 i + 1 个查询后,从城市 0 到城市 n - 1 的最短路径的长度。
示例 1:


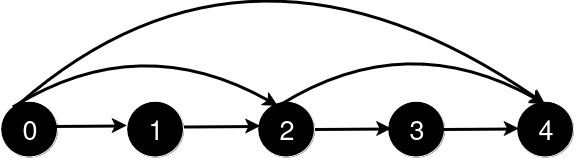
输入: n = 5, queries = [[2, 4], [0, 2], [0, 4]]
输出: [3, 2, 1]
解释:
新增一条从 2 到 4 的道路后,从 0 到 4 的最短路径长度为 3。
新增一条从 0 到 2 的道路后,从 0 到 4 的最短路径长度为 2。
新增一条从 0 到 4 的道路后,从 0 到 4 的最短路径长度为 1。示例 2:
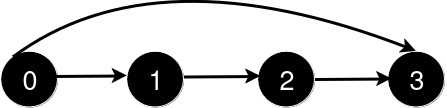
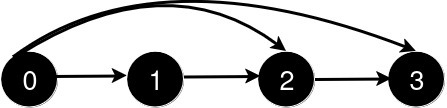
输入: n = 4, queries = [[0, 3], [0, 2]]
输出: [1, 1]
解释:
新增一条从 0 到 3 的道路后,从 0 到 3 的最短路径长度为 1。
新增一条从 0 到 2 的道路后,从 0 到 3 的最短路径长度仍为 1。说明:
- 3 <= n <= 10^5
- 1 <= queries.length <= 10^5
- queries[i].length == 2
- 0 <=
queries[i][0] < queries[i][1]< n - 1 <
queries[i][1] - queries[i][0] - 查询中不存在重复的道路。
- 不存在两个查询都满足 i != j 且
queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。
思路
有 n 个城市,刚开始每一个城市 i 有一条单项道路通向城市 i + 1,有一个二维数组 queries,queries[i] 表示增加一条从 queries[i][0] 到 queries[i][1] 的单项道路,返回 answer 数组,answer[i] 表示增加了 queries[i] 之后从城市 0 到城市 n - 1 的最短路径。增加的路径保证不会出现相交的情况。
比昨天的题 3243.新增道路查询后的最短距离I 多了一个条件,新增的路径不会交叉。昨天首先考虑的就是今天这个思路,因为起点与终点是固定的,可以通过查询区间的关系来减小最短路径。当时考虑的差分数组解决不了区间包含的关系。
定义区间数组 interval,interval[i] = j, 表示 i -> j 有直达道路。如果发现查询的路径 [l, r] 已经被包含,直接略过。否则,循环记录区间 (l, r) 内的路径数,保存下一跳的城市 next = interval[l],将 interval[l] 置为 r,l = next 直到 l >= r。注意最后一跳到 r 是没有计数的,相当于减去了将前面多余的步数,与直达的效果一样。 interval[l] = r 是第一次进入循环必须进行的操作,幸运的是它并不影响我们标记其它区间内的元素,当有更大的查询路径时,直接在 l 处就跳过了。
核心点是如何表示区间,如何判断区间是否重合,如何针对大区间减少的路径计数。
代码
/**
* @date 2024-11-20 10:10
*/
public class ShortestDistanceAfterQueries3244 {
public int[] shortestDistanceAfterQueries(int n, int[][] queries) {
int ql = queries.length;
int[] res = new int[ql];
int[] interval = new int[n - 1];
Arrays.setAll(interval, i -> i + 1);
int shortestPath = n - 1;
for (int i = 0; i < ql; i++) {
int l = queries[i][0];
int r = queries[i][1];
while (interval[l] < r) {
int next = interval[l];
interval[l] = r;
l = next;
shortestPath--;
}
res[i] = shortestPath;
}
return res;
}
}
性能