目标
给你一个整数 n 和一个二维整数数组 queries。
有 n 个城市,编号从 0 到 n - 1。初始时,每个城市 i 都有一条单向道路通往城市 i + 1( 0 <= i < n - 1)。
queries[i] = [ui, vi] 表示新建一条从城市 ui 到城市 vi 的单向道路。每次查询后,你需要找到从城市 0 到城市 n - 1 的最短路径的长度。
返回一个数组 answer,对于范围 [0, queries.length - 1] 中的每个 i,answer[i] 是处理完前 i + 1 个查询后,从城市 0 到城市 n - 1 的最短路径的长度。
示例 1:


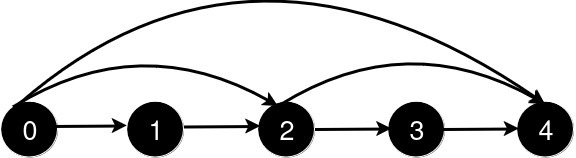
输入: n = 5, queries = [[2, 4], [0, 2], [0, 4]]
输出: [3, 2, 1]
解释:
新增一条从 2 到 4 的道路后,从 0 到 4 的最短路径长度为 3。
新增一条从 0 到 2 的道路后,从 0 到 4 的最短路径长度为 2。
新增一条从 0 到 4 的道路后,从 0 到 4 的最短路径长度为 1。示例 2:
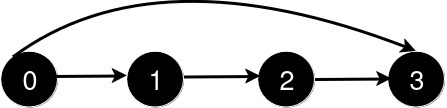
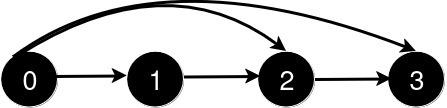
输入: n = 4, queries = [[0, 3], [0, 2]]
输出: [1, 1]
解释:
新增一条从 0 到 3 的道路后,从 0 到 3 的最短路径长度为 1。
新增一条从 0 到 2 的道路后,从 0 到 3 的最短路径长度仍为 1。说明:
- 3 <= n <= 500
- 1 <= queries.length <= 500
- queries[i].length == 2
- 0 <=
queries[i][0] < queries[i][1]< n - 1 <
queries[i][1] - queries[i][0] - 查询中没有重复的道路。
思路
有 n 个城市,刚开始每一个城市 i 有一条单项道路通向城市 i + 1,有一个二维数组 queries,queries[i] 表示增加一条从 queries[i][0] 到 queries[i][1] 的单项道路,返回 answer 数组,answer[i] 表示增加了 queries[i] 之后从城市 0 到城市 n - 1 的最短路径。
建图,每次增加路径之后使用BFS计算最短路径。注意过滤重复元素,否则过不了。
也可以使用动态规划来做。
定义 dp[i] 表示从城市 i 到城市 n - 1 的最短路径,每添加一条路径,受影响的只有包括起点在内前面的城市。当增加一条道路 [l, r],状态转移方程为 dp[l] = Math.min(dp[r] + 1, dp[l]),表示从 r 到达终点加一步 与 原来值的最小值。我们需要同步更新 l 之前的 dp 值。我们可以倒序遍历 [0, l),dp[j] = Math.min(dp[j], dp[j + 1] + 1) 取其自身与 后面元素 dp 值加一的较小值,同时还要考虑区间内有前面查询新增的道路,比如前面有以 j 为起点的查询,还要再取一个较小值 Math.min(dp[j], dp[end] + 1),end 表示之前增加的道路的终点。
代码
/**
* @date 2024-11-19 0:47
*/
public class ShortestDistanceAfterQueries3243 {
public int[] shortestDistanceAfterQueries_v2(int n, int[][] queries) {
int[] dp = new int[n];
int ql = queries.length;
int[] res = new int[ql];
for (int i = 0; i < n; i++) {
dp[i] = n - i - 1;
}
Map<Integer, List<Integer>> map = new HashMap<>(ql);
for (int i = 0; i < ql; i++) {
int l = queries[i][0];
int r = queries[i][1];
dp[l] = Math.min(dp[r] + 1, dp[l]);
for (int j = l - 1; j >= 0; j--) {
dp[j] = Math.min(dp[j], dp[j + 1] + 1);
if (map.containsKey(j)) {
for (Integer end : map.get(j)) {
dp[j] = Math.min(dp[j], dp[end] + 1);
}
}
}
res[i] = dp[0];
map.putIfAbsent(l, new ArrayList<>());
map.get(l).add(r);
}
return res;
}
public int[] shortestDistanceAfterQueries_v1(int n, int[][] queries) {
List<Integer>[] g = new ArrayList[n];
for (int i = 0; i < g.length; i++) {
g[i] = new ArrayList<>();
g[i].add(i + 1);
}
int ql = queries.length;
int[] res = new int[ql];
for (int i = 0; i < ql; i++) {
g[queries[i][0]].add(queries[i][1]);
res[i] = bfs_v1(g);
}
return res;
}
public int bfs_v1(List<Integer>[] g) {
int n = g.length;
List<Integer> list = new ArrayList<>();
boolean[] visited = new boolean[n];
list.add(0);
for (int res = 1; ; res++) {
List<Integer> tmp = list;
int size = tmp.size();
list = new ArrayList<>();
for (int i = 0; i < size; i++) {
Integer cur = tmp.get(i);
for (Integer next : g[cur]) {
if (next == n - 1) {
return res;
}
if (!visited[next]) {
visited[next] = true;
list.add(next);
}
}
}
}
}
public int[] shortestDistanceAfterQueries(int n, int[][] queries) {
List<Integer>[] g = new ArrayList[n];
for (int i = 0; i < g.length; i++) {
g[i] = new ArrayList<>();
g[i].add(i + 1);
}
int ql = queries.length;
int[] res = new int[ql];
for (int i = 0; i < ql; i++) {
g[queries[i][0]].add(queries[i][1]);
res[i] = bfs(g);
}
return res;
}
public int bfs(List<Integer>[] g) {
int res = 0, n = g.length;
Queue<Integer> q = new ArrayDeque<>();
q.offer(0);
here:
while (!q.isEmpty()) {
int size = q.size();
Set<Integer> set = new HashSet<>();
for (int i = 0; i < size; i++) {
int cur = q.poll();
if (cur == n - 1) {
break here;
}
set.addAll(g[cur]);
}
q.addAll(set);
res++;
}
return res;
}
}
性能