目标
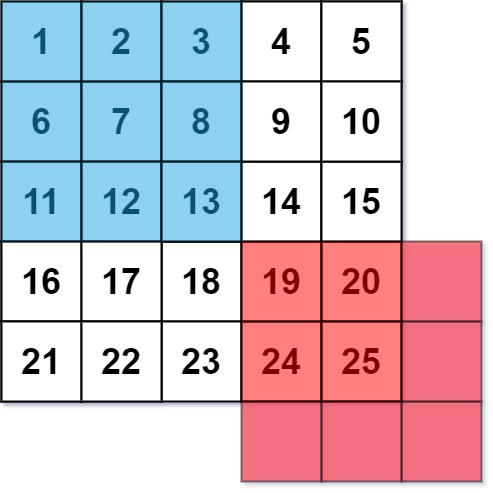
图像平滑器 是大小为 3 x 3 的过滤器,用于对图像的每个单元格平滑处理,平滑处理后单元格的值为该单元格的平均灰度。
每个单元格的 平均灰度 定义为:该单元格自身及其周围的 8 个单元格的平均值,结果需向下取整。(即,需要计算蓝色平滑器中 9 个单元格的平均值)。
如果一个单元格周围存在单元格缺失的情况,则计算平均灰度时不考虑缺失的单元格(即,需要计算红色平滑器中 4 个单元格的平均值)。
给你一个表示图像灰度的 m x n 整数矩阵 img ,返回对图像的每个单元格平滑处理后的图像 。
示例 1:
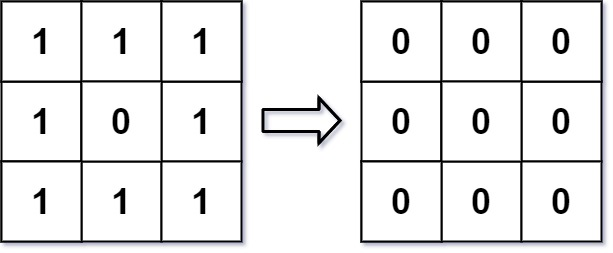
输入:img = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[0, 0, 0],[0, 0, 0], [0, 0, 0]]
解释:
对于点 (0,0), (0,2), (2,0), (2,2): 平均(3/4) = 平均(0.75) = 0
对于点 (0,1), (1,0), (1,2), (2,1): 平均(5/6) = 平均(0.83333333) = 0
对于点 (1,1): 平均(8/9) = 平均(0.88888889) = 0示例 2:
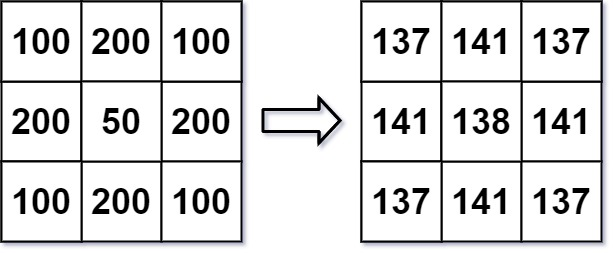
输入: img = [[100,200,100],[200,50,200],[100,200,100]]
输出: [[137,141,137],[141,138,141],[137,141,137]]
解释:
对于点 (0,0), (0,2), (2,0), (2,2): floor((100+200+200+50)/4) = floor(137.5) = 137
对于点 (0,1), (1,0), (1,2), (2,1): floor((200+200+50+200+100+100)/6) = floor(141.666667) = 141
对于点 (1,1): floor((50+200+200+200+200+100+100+100+100)/9) = floor(138.888889) = 138说明:
- m == img.length
- n == img[i].length
- 1 <= m, n <= 200
0 <= img[i][j] <= 255
思路
将图像中任意像素点的灰度值变为其自身以及周围八个像素灰度值的平均值。
可以使用二维前缀和,prefix[i][j] 表示左上顶点为 (0, 0) 右下顶点为 (i, j) 的矩形内的所有元素和。左上顶点为 (p, q) 右下顶点为 (i, j) 的矩形内所有元素和为 prefix[i][j] - prefix[i][q] - prefix[p][j] + prefix[p][q]。注意这里的坐标是顶点的坐标,而题目中的坐标表示格子的坐标,这样定义的前缀和表示以该格子为右下顶点的所有元素和,包括格子所在行列。
使用前缀和时多初始化一行一列可以大大简化代码逻辑,否则我们需要单独初始化第一行,第一列,并且需要在计算二维前缀和时判断下标越界。定义 prefix[i][j] 表示对角线 (0, 0) ~ (i - 1, j - 1) 矩形内的元素和,对于 m x n 矩阵,prefix[m][n] 表示所有元素和。以 (p, q) 为左上顶点,(i, j) 为右下顶点的前缀和为 prefix[i + 1][j + 1] - prefix[i + 1][q] - prefix[p][j + 1] + prefix[p][q]。
代码
/**
* @date 2024-11-18 9:10
*/
public class ImageSmoother661 {
public int[][] imageSmoother_v1(int[][] img) {
int m = img.length;
int n = img[0].length;
int[][] prefix = new int[m + 1][n + 1];
for (int r = 1; r <= m; r++) {
for (int c = 1; c <= n; c++) {
prefix[r][c] = prefix[r - 1][c] + prefix[r][c - 1] - prefix[r - 1][c - 1] + img[r - 1][c - 1];
}
}
for (int r = 0; r < m; r++) {
int i = Math.min(m - 1, r + 1);
int p = Math.max(0, r - 1);
for (int c = 0; c < n; c++) {
int j = Math.min(n - 1, c + 1);
int q = Math.max(0, c - 1);
int cnt = (i - p + 1) * (j - q + 1);
img[r][c] = (prefix[i + 1][j + 1] - prefix[p][j + 1] - prefix[i + 1][q] + prefix[p][q]) / cnt;
}
}
return img;
}
}
性能