日期: 2024 年 11 月 14 日

目标

现有一棵 无向 树，树中包含 n 个节点，按从 0 到 n - 1 标记。树的根节点是节点 0 。给你一个长度为 n - 1 的二维整数数组 edges，其中 edges[i] = [ai, bi] 表示树中节点 ai 与节点 bi 之间存在一条边。

如果一个节点的所有子节点为根的 子树 包含的节点数相同，则认为该节点是一个 好节点。

返回给定树中 好节点 的数量。

子树 指的是一个节点以及它所有后代节点构成的一棵树。

示例 1：

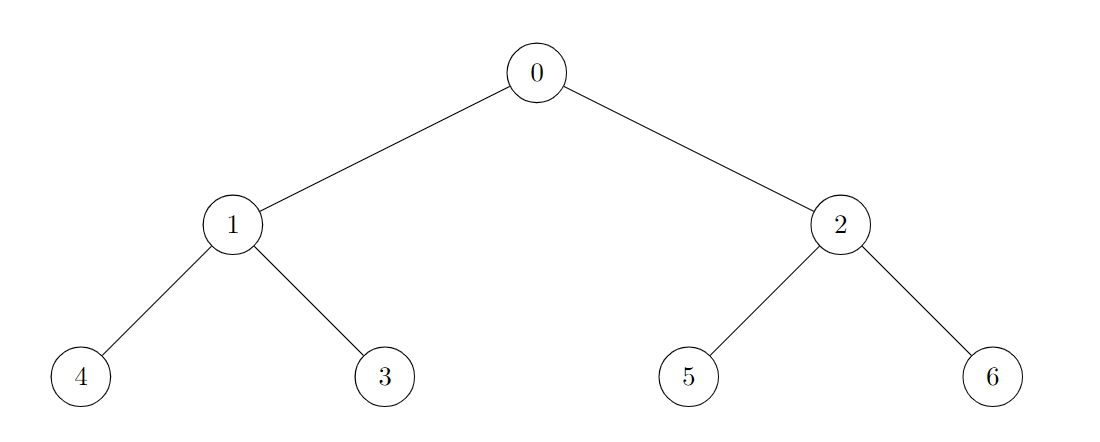
输入：edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
输出：7
说明：
树的所有节点都是好节点。

示例 2：

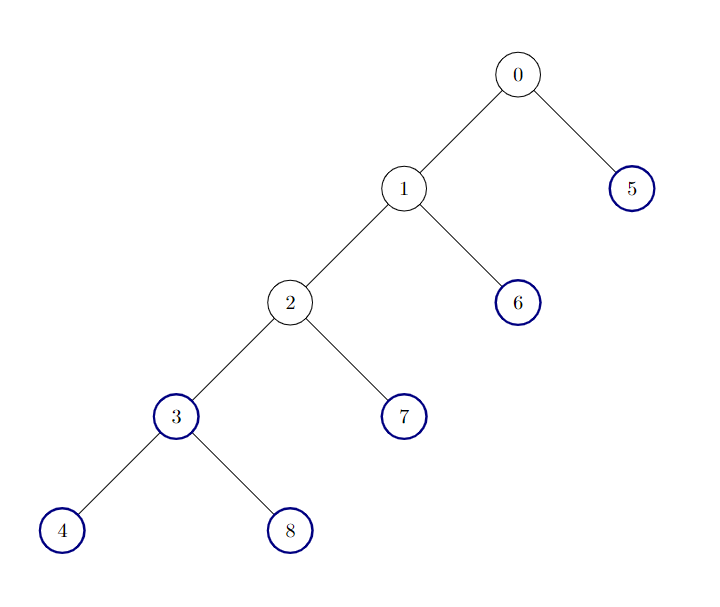
输入：edges = [[0,1],[1,2],[2,3],[3,4],[0,5],[1,6],[2,7],[3,8]]
输出：6
说明：
树中有 6 个好节点。上图中已将这些节点着色。

示例 3：

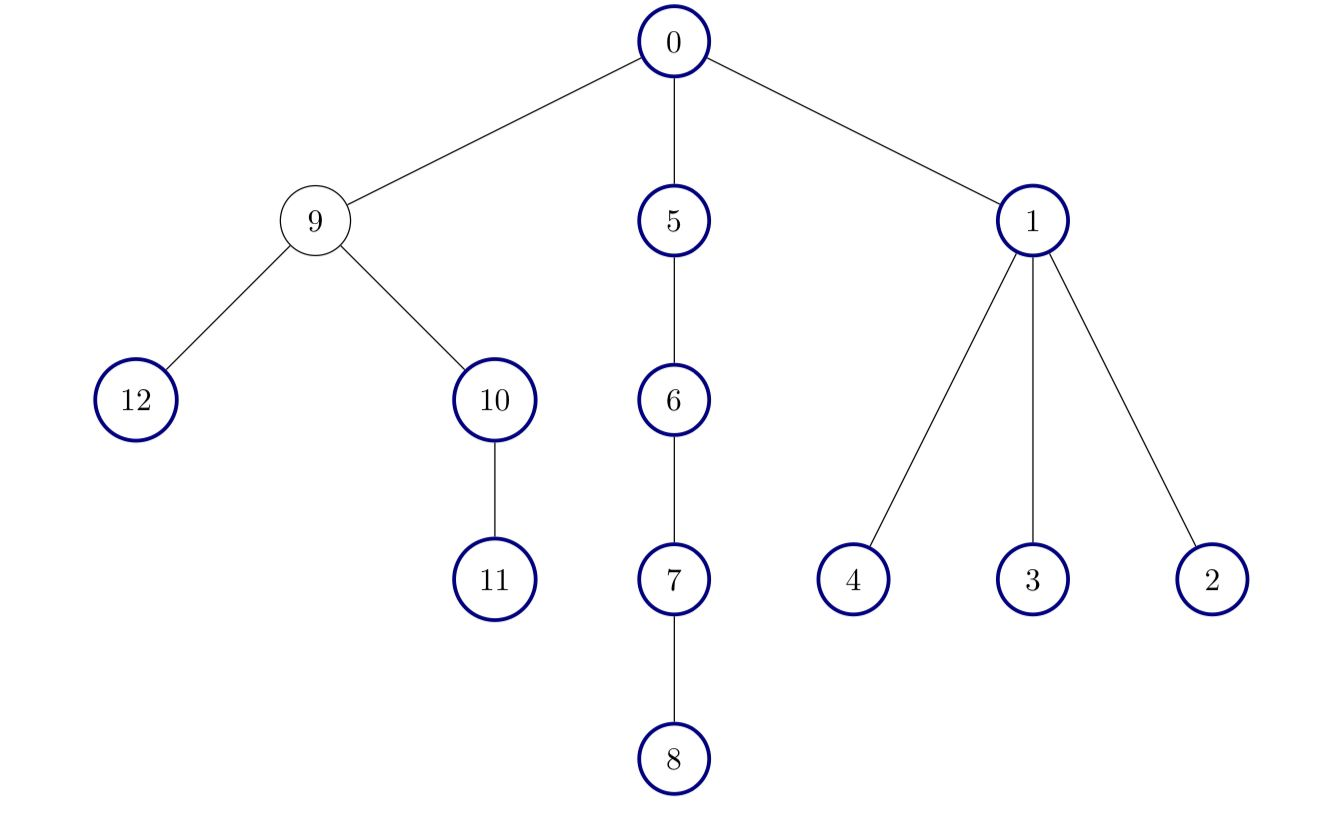
输入：edges = [[0,1],[1,2],[1,3],[1,4],[0,5],[5,6],[6,7],[7,8],[0,9],[9,10],[9,12],[10,11]]
输出：12
解释：
除了节点 9 以外其他所有节点都是好节点。

说明：

• 2 <= n <= 10^5
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• 输入确保 edges 总表示一棵有效的树。

思路

树中的任一节点，如果以它的子节点为根的子树包含相同的节点数量，则称该节点为好节点。注意没有要求子节点是好节点，只统计子树整体的节点个数。求给定树的好节点个数。

dfs 获取子树节点数目，判断各子树的节点个数是否相同。叶子节点没有子树，可认为子树节点个数为 0 也是好节点。

代码

/**
 * @date 2024-11-14 9:32
 */
public class CountGoodNodes3249 {
    int res = 0;
    List<Integer>[] g;

    public int countGoodNodes(int[][] edges) {
        g = new List[edges.length + 1];
        int n = g.length;
        for (int i = 0; i < n; i++) {
            g[i] = new ArrayList<>();
        }
        for (int i = 0; i < edges.length; i++) {
            g[edges[i][0]].add(edges[i][1]);
            g[edges[i][1]].add(edges[i][0]);
        }
        dfs(-1, 0);
        return res;
    }

    public int dfs(int parent, int cur) {
        int num = 1;
        int prev = -1;
        boolean equal = true;
        for (Integer next : g[cur]) {
            if (next == parent) {
                continue;
            }
            int childNum = dfs(cur, next);
            if (prev != -1 && prev != childNum) {
                equal = false;
            }
            prev = childNum;
            num += childNum;
        }
        if (equal) {
            res++;
        }
        return num;
    }

}

性能