目标
给你一个 n x n 的二维数组 grid,它包含范围 [0, n^2 - 1] 内的不重复元素。
实现 neighborSum 类:
- neighborSum(int [][]grid) 初始化对象。
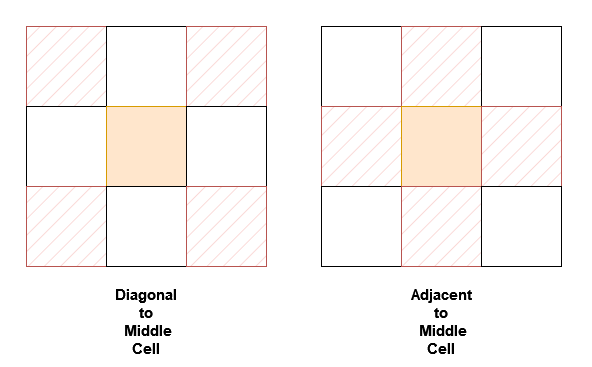
- int adjacentSum(int value) 返回在 grid 中与 value 相邻的元素之和,相邻指的是与 value 在上、左、右或下的元素。
- int diagonalSum(int value) 返回在 grid 中与 value 对角线相邻的元素之和,对角线相邻指的是与 value 在左上、右上、左下或右下的元素。
示例 1:
输入:
["neighborSum", "adjacentSum", "adjacentSum", "diagonalSum", "diagonalSum"]
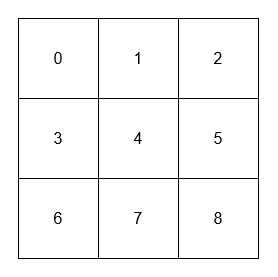
[[[[0, 1, 2], [3, 4, 5], [6, 7, 8]]], [1], [4], [4], [8]]
输出: [null, 6, 16, 16, 4]
解释:
1 的相邻元素是 0、2 和 4。
4 的相邻元素是 1、3、5 和 7。
4 的对角线相邻元素是 0、2、6 和 8。
8 的对角线相邻元素是 4。示例 2:
输入:
["neighborSum", "adjacentSum", "diagonalSum"]
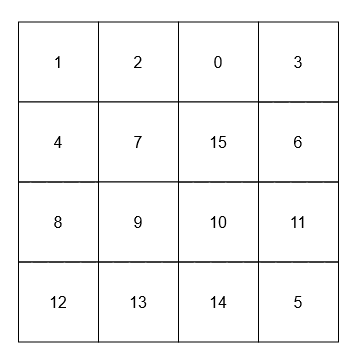
[[[[1, 2, 0, 3], [4, 7, 15, 6], [8, 9, 10, 11], [12, 13, 14, 5]]], [15], [9]]
输出: [null, 23, 45]
解释:
15 的相邻元素是 0、10、7 和 6。
9 的对角线相邻元素是 4、12、14 和 15。说明:
- 3 <= n == grid.length == grid[0].length <= 10
0 <= grid[i][j] <= n^2 - 1- 所有
grid[i][j]值均不重复。 - adjacentSum 和 diagonalSum 中的 value 均在范围 [0, n^2 - 1] 内。
- 最多会调用 adjacentSum 和 diagonalSum 总共 2 * n^2 次。
思路
有一个 n x n 的二维矩阵,其元素值的范围是 0 ~ n^2 - 1,且元素值互不相同。给定一个元素值,求其上下左右的元素和以及对角线元素和(左上、右上、左下和右下)。
首先要找到这个给定的元素,再根据其下标计算元素和,对于大量重复地查询,可以记录每个元素值对应的下标。
每次定位的时间复杂度为 100,由于存在缓存,最多搜索 100 次,总复杂度为 10^4。
我们也可以在初始化的时候直接建立 元素值 与 坐标的映射,时间复杂度降为 O(n^2) 即 100。
还可以进一步优化,由于数据值是不可变的,可以提前将 相邻元素和 都计算好,查的时候无需重复计算。此外,由于元素各不相同,可以直接将元素值映射为下标,将元素值与坐标的映射改为元素值与相邻元素和的映射。
代码
/**
* @date 2024-11-09 11:21
*/
public class NeighborSum3242 {
class NeighborSum {
int[][] adjacent = new int[][]{
new int[]{-1, 0},
new int[]{1, 0},
new int[]{0, -1},
new int[]{0, 1},
};
int[][] diagonal = new int[][]{
new int[]{-1, -1},
new int[]{-1, 1},
new int[]{1, -1},
new int[]{1, 1},
};
int[] adjacentSum;
int[] diagonalSum;
public NeighborSum(int[][] grid) {
int index = 0;
int n = grid.length;
int length = n * n;
adjacentSum = new int[length];
diagonalSum = new int[length];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
int value = grid[i][j];
adjacentSum[value] = sum(grid, i, j, adjacent);
diagonalSum[value] = sum(grid, i, j, diagonal);
}
}
}
public int adjacentSum(int value) {
return adjacentSum[value];
}
public int diagonalSum(int value) {
return diagonalSum[value];
}
private int sum(int[][] grid, int i, int j, int[][] directions){
int res = 0;
for (int[] direction : directions) {
int row = direction[0] + i;
int col = direction[1] + j;
if (row < 0 || col < 0 || row >= grid.length || col >= grid.length) {
continue;
}
res += grid[row][col];
}
return res;
}
}
}
性能