目标
在本问题中,有根树指满足以下条件的 有向 图。该树只有一个根节点,所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点。
输入一个有向图,该图由一个有着 n 个节点(节点值不重复,从 1 到 n)的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间,这条附加的边不属于树中已存在的边。
结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi],用以表示 有向 图中连接顶点 ui 和顶点 vi 的边,其中 ui 是 vi 的一个父节点。
返回一条能删除的边,使得剩下的图是有 n 个节点的有根树。若有多个答案,返回最后出现在给定二维数组的答案。
示例 1:
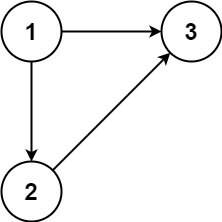
输入:edges = [[1,2],[1,3],[2,3]]
输出:[2,3]示例 2:
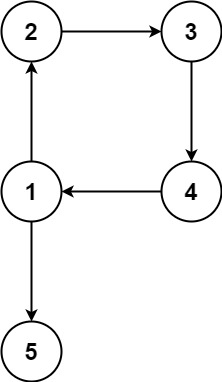
输入:edges = [[1,2],[2,3],[3,4],[4,1],[1,5]]
输出:[4,1]说明:
- n == edges.length
- 3 <= n <= 1000
- edges[i].length == 2
- 1 <= ui, vi <= n
思路
有一颗 n 个节点的树,节点编号 1 ~ n。使用 edges 表示向树中两个没有直接连接的节点之间加一条边之后的边的集合,找出一条可以删除的边使得 edges 变为一颗有 n 个节点的树。如果有多种选择,返回 edges 中最后出现的那个,即下标最大的边。与 冗余连接 不同的是 edges 是 有向边 的集合。
如果直接使用昨天无向图寻找环的做法会有两个问题:
- 无法处理 a -> b, b -> a 的情况,因为在无向图中为了防止环,直接回避了这种情况
- 并不是删去环上任意一条边都可以的,因为边是有向的,如果某个节点出现两个父节点,那么一定要删去以该节点为终点的边
官网题解使用的还是并查集。// todo
代码
/**
* @date 2024-10-28 8:51
*/
public class FindRedundantDirectedConnection685 {
List<Integer>[] g;
Set<Integer> loop;
List<Integer> path;
int start;
int end;
public int[] findRedundantDirectedConnection(int[][] edges) {
int n = edges.length;
g = new List[n + 1];
for (int i = 0; i <= n; i++) {
g[i] = new ArrayList<>();
}
int[] degree = new int[n + 1];
Set<Integer> e = new HashSet<>(n);
int end = -1;
int[] self = null;
for (int[] edge : edges) {
int from = edge[0];
int to = edge[1];
int fromto = from << 10 | to;
int tofrom = to << 10 | from;
if (e.contains(fromto)) {
self = new int[]{from, to};
}
e.add(fromto);
e.add(tofrom);
g[from].add(to);
g[to].add(from);
if (degree[to] == 1) {
end = to;
} else {
degree[to]++;
}
}
if (self != null) {
if (end == -1) {
for (int i = n - 1; i >= 0; i--) {
if ((self[0] == edges[i][0] && edges[i][1] == self[1])
|| (self[0] == edges[i][1] && edges[i][0] == self[1])) {
return edges[i];
}
}
} else {
return new int[]{self[0] == end ? self[1] : self[0], end};
}
}
loop = new HashSet<>(n);
path = new ArrayList<>();
loop.add(1);
path.add(1);
dfs(0, 1);
loop = new HashSet<>();
for (int i = path.size() - 1; i >= 0; i--) {
loop.add(path.get(i));
if (start == path.get(i)) {
break;
}
}
if (end == -1) {
for (int i = n - 1; i >= 0; i--) {
if (loop.contains(edges[i][0]) && loop.contains(edges[i][1])) {
return edges[i];
}
}
} else {
for (int i = n - 1; i >= 0; i--) {
if (edges[i][1] == end && loop.contains(edges[i][0])) {
return edges[i];
}
}
}
return null;
}
private boolean dfs(int parent, int current) {
for (Integer next : g[current]) {
if (next == parent) {
continue;
}
if (loop.contains(next)) {
start = next;
return true;
} else {
loop.add(next);
path.add(next);
if (dfs(current, next)) {
return true;
}
path.remove(path.size() - 1);
loop.remove(next);
}
}
return false;
}
}
性能