目标
给你一个下标从 0 开始长度为 n 的整数数组 buses ,其中 buses[i] 表示第 i 辆公交车的出发时间。同时给你一个下标从 0 开始长度为 m 的整数数组 passengers ,其中 passengers[j] 表示第 j 位乘客的到达时间。所有公交车出发的时间互不相同,所有乘客到达的时间也互不相同。
给你一个整数 capacity ,表示每辆公交车 最多 能容纳的乘客数目。
每位乘客都会搭乘下一辆有座位的公交车。如果你在 y 时刻到达,公交在 x 时刻出发,满足 y <= x 且公交没有满,那么你可以搭乘这一辆公交。最早 到达的乘客优先上车。
返回你可以搭乘公交车的最晚到达公交站时间。你 不能 跟别的乘客同时刻到达。
注意:数组 buses 和 passengers 不一定是有序的。
示例 1:
输入:buses = [10,20], passengers = [2,17,18,19], capacity = 2
输出:16
解释:
第 1 辆公交车载着第 1 位乘客。
第 2 辆公交车载着你和第 2 位乘客。
注意你不能跟其他乘客同一时间到达,所以你必须在第二位乘客之前到达。
示例 2:
输入:buses = [20,30,10], passengers = [19,13,26,4,25,11,21], capacity = 2
输出:20
解释:
第 1 辆公交车载着第 4 位乘客。
第 2 辆公交车载着第 6 位和第 2 位乘客。
第 3 辆公交车载着第 1 位乘客和你。
说明:
- n == buses.length
- m == passengers.length
- 1 <= n, m, capacity <= 10^5
- 2 <= buses[i], passengers[i] <= 10^9
- buses 中的元素 互不相同 。
- passengers 中的元素 互不相同 。
思路
已知某路公交车的最大容量 capacity,离开时间数组 buses,以及乘客到达时间数组 passengers。离开/到达 时间是整数,乘客的到达时间各不相同,自己的到达时间也不能与其它乘客重复,问能够赶上公交的最晚到达时间。
刚开始想到了二分查找,理论上来说只要在 0 ~ buses[n - 1] 内找到不与 passengers 重复的最大值即可。但是问题在于,如果与其它乘客的到达时间重复了,我们该如何缩小范围呢?向左找还是向右找?这个是不确定的,二分查找需要能够明确地排除一半的数据范围,这里是做不到的。
我们也不能直接从小于 buses[n - 1] 的乘客开始向前枚举,因为车的容量是有限的,如果前面积压的乘客过多,后面的乘客照样上不了车。
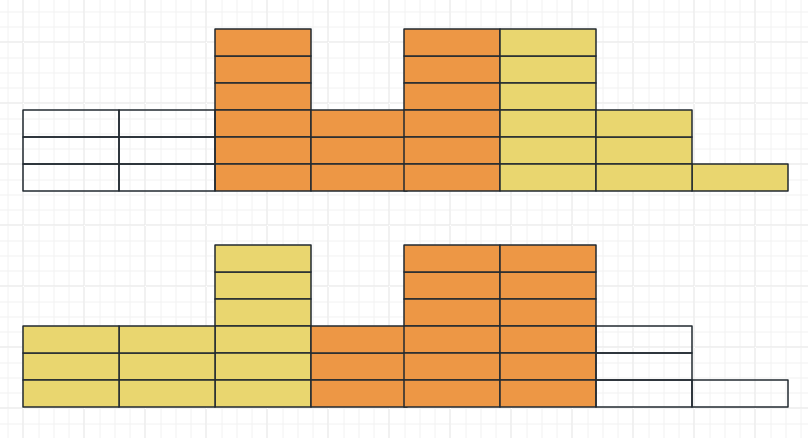
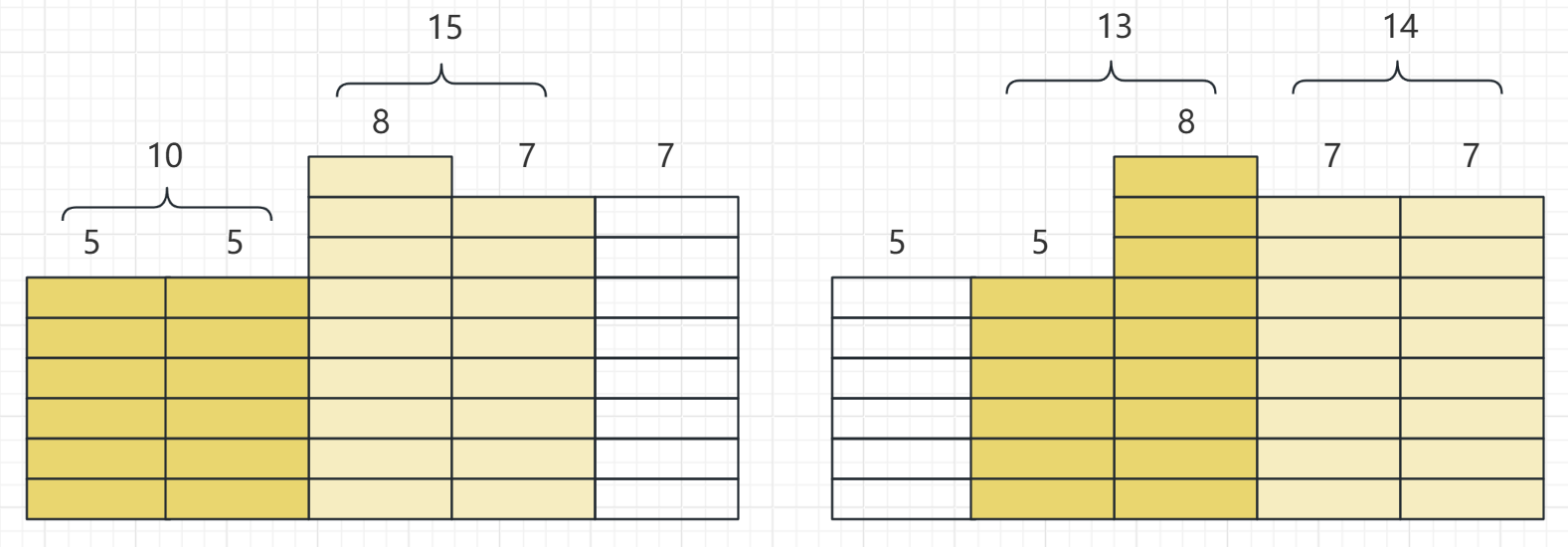
如果没有限制条件,我们只需要作为最后一班车的最后一名乘客上车即可。但这里要求到达时间不能与其它乘客相同,如果已经有乘客在最后一班车准备离开时到达,我们无法作为最后一名乘客上车。考虑这种极端情况,公交到达时间为 5 10 15 容量为5,乘客到达时间为 2 3 4 5 6 | 7 8 9 10 11 | 12 13 14 15 16 我们必须在时间 1 之前到达,其它时间会与乘客到达时间相同或者赶不上公交。
我们可以首先将公交的离开时间以及乘客的到达时间排序,然后枚举每一辆公交,如果 passengers[i] <= buses[j] && capacity > 0 就可以上车,并将 capacity-- 。车满了或者没有剩余乘客在当前公交离开时间之前到达,将 capacity 重置,等待下一班车。然后我们判断最后一班车是否有剩余位置,如果有则取 buses[n - 1],否则取最后一位上车的乘客到达时间。最后判断是否与最后一名上车的乘客的到达时间相同,如果相同,则将时间减一并与倒数第二名上车的乘客到达时间比较,以此类推。最开始使用了哈希表保存了乘客的到达时间,然后判断是否在集合内,其实没有必要,因为乘客到达时间数组已经排过序了,依次从后向前找如果不相等则一定不在数组中。
最后的处理有许多细节,比如不能直接取最后一名乘客的到达时间减1,需要判断是否有空位;如果有空位不能直接返回buses[n - 1],需要判断是否重复;最开始是外层枚举乘客,内层枚举公交车,这样会漏掉乘客枚举完但还剩余公交车的情况,这时最后一名乘客不能算入最后一班车的位置,等等。
代码
/**
* @date 2024-09-18 10:41
*/
public class LatestTimeCatchTheBus2332 {
public int latestTimeCatchTheBus_v2(int[] buses, int[] passengers, int capacity) {
Arrays.sort(buses);
Arrays.sort(passengers);
int n = buses.length;
int m = passengers.length;
int i = 0, j = 0, cnt = capacity;
for (; i < n; i++) {
cnt = capacity;
while (cnt > 0 && j < m && passengers[j] <= buses[i]) {
cnt--;
j++;
}
}
int res;
j--;
if (cnt > 0) {
res = buses[n - 1];
} else {
res = passengers[j];
}
while (j >= 0 && passengers[j] == res) {
res--;
j--;
}
return res;
}
}
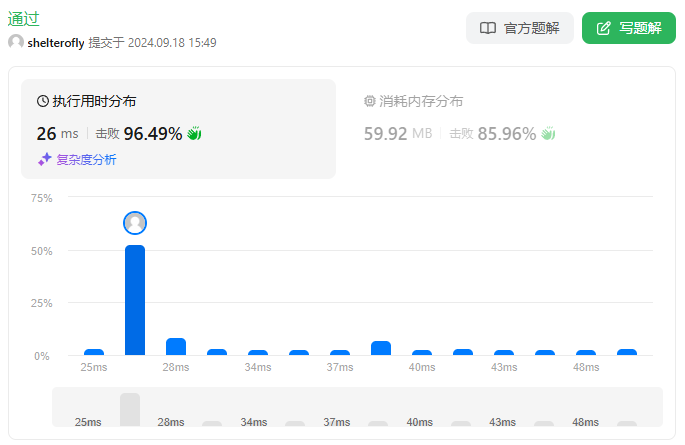
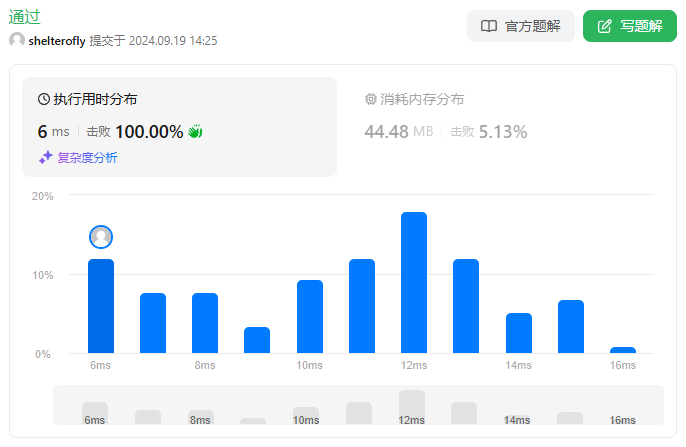
性能