目标
给你一个有向图,图中有 n 个节点,节点编号从 0 到 n - 1 ,其中每个节点都 恰有一条 出边。
图由一个下标从 0 开始、长度为 n 的整数数组 edges 表示,其中 edges[i] 表示存在一条从节点 i 到节点 edges[i] 的 有向 边。
节点 i 的 边积分 定义为:所有存在一条指向节点 i 的边的节点的 编号 总和。
返回 边积分 最高的节点。如果多个节点的 边积分 相同,返回编号 最小 的那个。
示例 1:
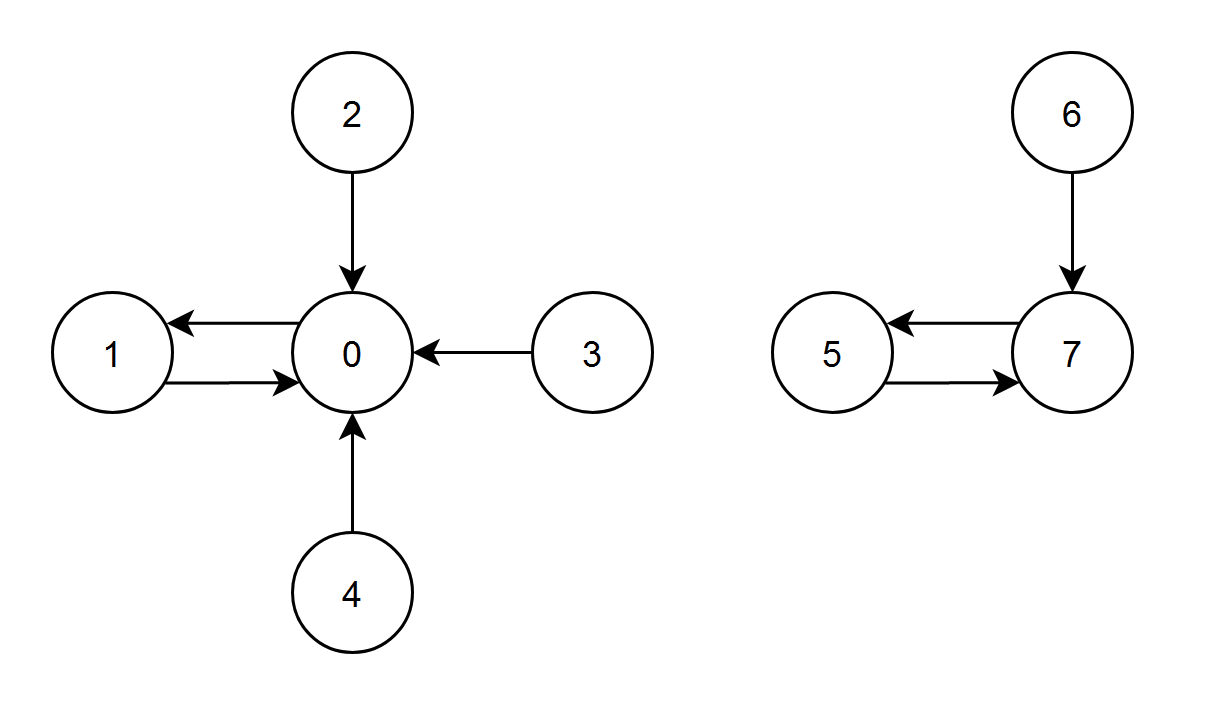
输入:edges = [1,0,0,0,0,7,7,5]
输出:7
解释:
- 节点 1、2、3 和 4 都有指向节点 0 的边,节点 0 的边积分等于 1 + 2 + 3 + 4 = 10 。
- 节点 0 有一条指向节点 1 的边,节点 1 的边积分等于 0 。
- 节点 7 有一条指向节点 5 的边,节点 5 的边积分等于 7 。
- 节点 5 和 6 都有指向节点 7 的边,节点 7 的边积分等于 5 + 6 = 11 。
节点 7 的边积分最高,所以返回 7 。示例 2:
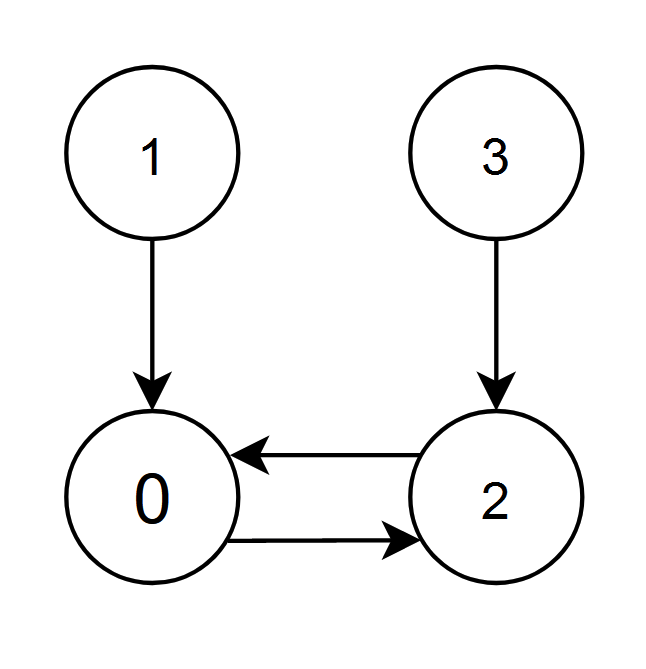
输入:edges = [2,0,0,2]
输出:0
解释:
- 节点 1 和 2 都有指向节点 0 的边,节点 0 的边积分等于 1 + 2 = 3 。
- 节点 0 和 3 都有指向节点 2 的边,节点 2 的边积分等于 0 + 3 = 3 。
节点 0 和 2 的边积分都是 3 。由于节点 0 的编号更小,返回 0 。说明:
- n == edges.length
- 2 <= n <= 10^5
- 0 <= edges[i] < n
- edges[i] != i
思路
有 n 个节点编号为 0 ~ n-1,每个节点都有一条边指向自己或者其它节点,edges[i] 表示节点 i 指向节点 edges[i]。节点的边积分定义为所有指向该节点的节点编号之和。求边积分最高的节点编号,如果相同则取编号最小的那个。
直接为被指向节点累加积分,取最大积分中编号最小的即可。容易出错的点是数据溢出,当所有节点都指向 0 节点时,边积分最大,其值为 1 ~ 最大节点编号n 求和 n(n+1)/2。编号最大为 100000,边积分最大值为 5000050000 需要使用 long 型计数。
代码
/**
* @date 2024-09-21 10:55
*/
public class EdgeScore2374 {
public int edgeScore(int[] edges) {
int n = edges.length;
long[] cnt = new long[n];
for (int i = 0; i < n; i++) {
cnt[edges[i]] += i;
}
int res = 0;
for (int i = 0; i < n; i++) {
if (cnt[i] > cnt[res]) {
res = i;
}
}
return res;
}
}
性能