目标
环形公交路线上有 n 个站,按次序从 0 到 n - 1 进行编号。我们已知每一对相邻公交站之间的距离,distance[i] 表示编号为 i 的车站和编号为 (i + 1) % n 的车站之间的距离。
环线上的公交车都可以按顺时针和逆时针的方向行驶。
返回乘客从出发点 start 到目的地 destination 之间的最短距离。
示例 1:
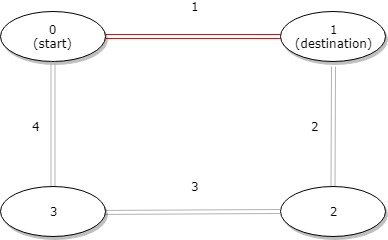
输入:distance = [1,2,3,4], start = 0, destination = 1
输出:1
解释:公交站 0 和 1 之间的距离是 1 或 9,最小值是 1。示例 2:
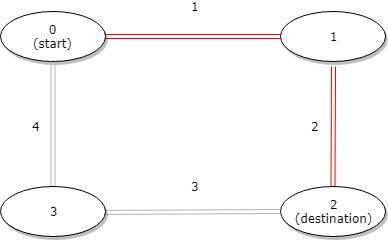
输入:distance = [1,2,3,4], start = 0, destination = 2
输出:3
解释:公交站 0 和 2 之间的距离是 3 或 7,最小值是 3。示例 3:

输入:distance = [1,2,3,4], start = 0, destination = 3
输出:4
解释:公交站 0 和 3 之间的距离是 6 或 4,最小值是 4。说明:
- 1 <= n <= 10^4
- distance.length == n
- 0 <= start, destination < n
- 0 <= distance[i] <= 10^4
思路
有一个数组 distance,元素 distance[i] 表示车站 i 到 车站 i + 1 的距离。环线上的车可以顺时针或逆时针行驶,求 start 到 destination 的最短距离。
假设,start <= destination。实际上是比较子数组 [start, destination - 1] 的元素和 与 子数组 [0, start - 1] [destination, n - 1] 的元素和,取其中的较小值。
由于是环形的,因此有可能 start > destination。注意处理初始条件,否则子数组 [start, destination - 1] 不合法,而 [0, start - 1] [destination, n - 1] 则覆盖了所有站点。
代码
/**
* @date 2024-09-16 20:08
*/
public class DistanceBetweenBusStops1184 {
public int distanceBetweenBusStops(int[] distance, int start, int destination) {
int n = distance.length;
int s = Math.min(start, destination);
int e = Math.max(start, destination);
int d1 = 0, d2 = 0;
for (int i = 0; i < n; i++) {
if (i < s || i >= e) {
d1 += distance[i];
} else {
d2 += distance[i];
}
}
return Math.min(d1, d2);
}
}
性能
