目标
给你一个由 正整数 组成、大小为 m x n 的矩阵 grid。你可以从矩阵中的任一单元格移动到另一个位于正下方或正右侧的任意单元格(不必相邻)。从值为 c1 的单元格移动到值为 c2 的单元格的得分为 c2 - c1 。
你可以从 任一 单元格开始,并且必须至少移动一次。
返回你能得到的 最大 总得分。
示例 1:
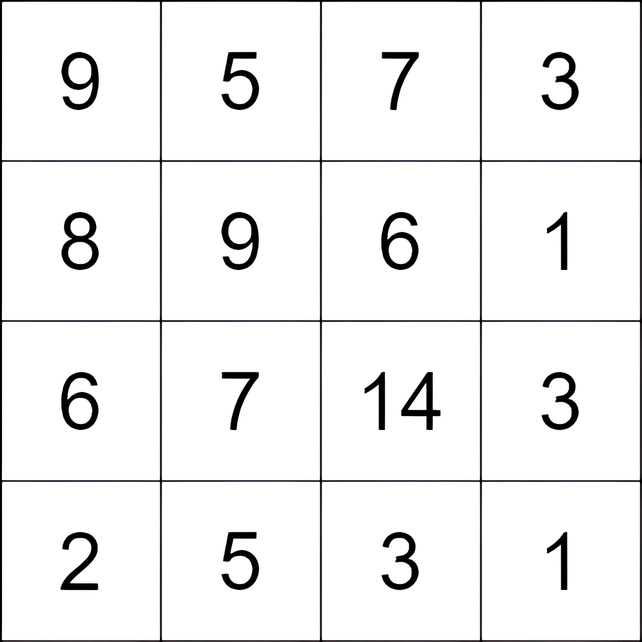
输入:grid = [[9,5,7,3],[8,9,6,1],[6,7,14,3],[2,5,3,1]]
输出:9
解释:从单元格 (0, 1) 开始,并执行以下移动:
- 从单元格 (0, 1) 移动到 (2, 1),得分为 7 - 5 = 2 。
- 从单元格 (2, 1) 移动到 (2, 2),得分为 14 - 7 = 7 。
总得分为 2 + 7 = 9 。
示例 2:
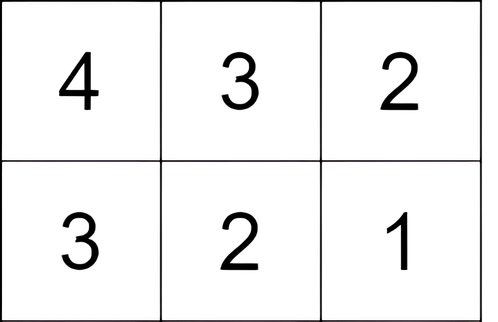
输入:grid = [[4,3,2],[3,2,1]]
输出:-1
解释:从单元格 (0, 0) 开始,执行一次移动:从 (0, 0) 到 (0, 1) 。得分为 3 - 4 = -1 。
说明:
- m == grid.length
- n == grid[i].length
- 2 <= m, n <= 1000
- 4 <= m * n <= 10^5
1 <= grid[i][j] <= 10^5
思路
有一个二维矩阵 grid,可以从任意格子出发向下或右移动(不必相邻),移动的得分为元素值之差 to - from,求最大的得分数。
首先想到动态规划,关键点是想清楚最大得分其实就是以当前元素为左上顶点(不包括其自身),以 m - 1, n - 1 为右下顶点的矩形中的最大值减去当前元素值。如果把状态定义错误还是会超时的,比如当前元素出发所能取得的最大值,需要依次向下/向右比较,时间复杂度 O(m * n * (m +n)),m = 1000 n = 95,循环次数 10^5 * (10^3 + 95) 超时,耗时878 ms,下午又提交了几次,耗时 1200 ~ 1300 ms。参考特殊数组II 中的时间复杂度分析。对于O(n)的算法,10^8 差不多就是极限了,单个用例在1s左右,多个肯定超时。
代码
/**
* @date 2024-08-15 0:22
*/
public class MaxScore3148 {
/**
* 修改了dp的定义,表示以i,j为起点到右下的矩形的最大值
* 执行通过
*/
public int maxScore_v2(List<List<Integer>> grid) {
int m = grid.size();
int n = grid.get(0).size();
int[][] dp = new int[m][n];
int res = Integer.MIN_VALUE;
dp[m - 1][n - 1] = grid.get(m - 1).get(n - 1);
for (int i = n - 2; i >= 0; i--) {
int cur = grid.get(m - 1).get(i);
// 注意这里使用的是上一个位置为顶点的矩形中的最大值
res = Math.max(dp[m - 1][i + 1] - cur, res);
// 如果先进行这个计算,然后再进行上面的计算,就有会出现不移动的情况,但积分只有移动才能取得,可以是负值
dp[m - 1][i] = Math.max(cur, dp[m - 1][i + 1]);
}
for (int i = m - 2; i >= 0; i--) {
int cur = grid.get(i).get(n - 1);
res = Math.max(dp[i + 1][n - 1] - cur, res);
dp[i][n - 1] = Math.max(cur, dp[i + 1][n - 1]);
}
for (int i = m - 2; i >= 0; i--) {
for (int j = n - 2; j >= 0; j--) {
int cur = grid.get(i).get(j);
res = Math.max(dp[i + 1][j] - cur, res);
res = Math.max(dp[i][j + 1] - cur, res);
dp[i][j] = Math.max(cur, dp[i + 1][j]);
dp[i][j] = Math.max(dp[i][j], dp[i][j + 1]);
}
}
return res;
}
/**
* 560 / 564 超时 m = 1000 n = 95
* O(m * n * (m +n)) 循环次数 10^5 * (10^3 + 95)
* 878 ms
*/
public int maxScore_v1(List<List<Integer>> grid) {
int m = grid.size();
int n = grid.get(0).size();
int[][] dp = new int[m][n];
for (int[] row : dp) {
Arrays.fill(row, Integer.MIN_VALUE);
}
dp[m - 1][n - 1] = 0;
int res = Integer.MIN_VALUE;
for (int i = n - 2; i >= 0; i--) {
for (int j = i + 1; j < n; j++) {
int diff = grid.get(m - 1).get(j) - grid.get(m - 1).get(i);
if (dp[m - 1][j] > 0) {
dp[m - 1][i] = Math.max(diff + dp[m - 1][j], dp[m - 1][i]);
}
dp[m - 1][i] = Math.max(diff, dp[m - 1][i]);
}
res = Math.max(dp[m - 1][i], res);
}
for (int i = m - 2; i >= 0; i--) {
for (int j = i + 1; j < m; j++) {
int diff = grid.get(j).get(n - 1) - grid.get(i).get(n - 1);
if (dp[j][n - 1] > 0) {
dp[i][n - 1] = Math.max(diff + dp[j][n - 1], dp[i][n - 1]);
}
dp[i][n - 1] = Math.max(diff, dp[i][n - 1]);
}
res = Math.max(dp[i][n - 1], res);
}
for (int i = m - 2; i >= 0; i--) {
for (int j = n - 2; j >= 0; j--) {
for (int h = i + 1; h < m; h++) {
int rowDiff = grid.get(h).get(j) - grid.get(i).get(j);
if (dp[h][j] > 0) {
dp[i][j] = Math.max(rowDiff + dp[h][j], dp[i][j]);
}
dp[i][j] = Math.max(rowDiff, dp[i][j]);
}
for (int k = j + 1; k < n; k++) {
int colDiff = grid.get(i).get(k) - grid.get(i).get(j);
if (dp[i][k] > 0) {
dp[i][j] = Math.max(colDiff + dp[i][k], dp[i][j]);
}
dp[i][j] = Math.max(colDiff, dp[i][j]);
}
res = Math.max(dp[i][j], res);
}
}
return res;
}
}
性能