日期: 2024 年 8 月 29 日

目标

给你一个大小为 m x n 的二维矩阵 grid 。你需要判断每一个格子 grid[i][j] 是否满足：

• 如果它下面的格子存在，那么它需要等于它下面的格子，也就是 grid[i][j] == grid[i + 1][j] 。
• 如果它右边的格子存在，那么它需要不等于它右边的格子，也就是 grid[i][j] != grid[i][j + 1] 。

如果 所有 格子都满足以上条件，那么返回 true ，否则返回 false 。

示例 1：

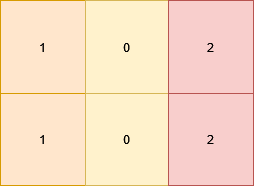
输入：grid = [[1,0,2],[1,0,2]]
输出：true
解释：
网格图中所有格子都符合条件。

示例 2：

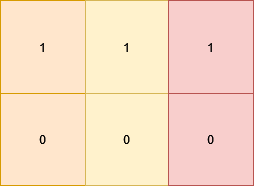
输入：grid = [[1,1,1],[0,0,0]]
输出：false
解释：
同一行中的格子值都相等。

示例 3：

输入：grid = [[1],[2],[3]]
输出：false
解释：
同一列中的格子值不相等。

说明：

• 1 <= n, m <= 10
• 0 <= grid[i][j] <= 9

思路

判断矩阵是否满足纵向元素都相等，横向相邻元素各不同。

代码

/**
 * @date 2024-08-29 0:07
 */
public class SatisfiesConditions3142 {

    public boolean satisfiesConditions(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        for (int i = 1; i < m; i++) {
            if (grid[i][0] != grid[i - 1][0]) {
                return false;
            }
        }
        for (int j = 1; j < n; j++) {
            if (grid[0][j] == grid[0][j - 1]) {
                return false;
            }
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (grid[i][j] == grid[i][j - 1] || grid[i][j] != grid[i - 1][j]) {
                    return false;
                }
            }
        }
        return true;
    }
}

性能