日期: 2024 年 7 月 31 日

目标

给你一个二维整数数组 point ，其中 points[i] = [xi, yi] 表示二维平面内的一个点。同时给你一个整数 w 。你需要用矩形 覆盖所有 点。

每个矩形的左下角在某个点 (x1, 0) 处，且右上角在某个点 (x2, y2) 处，其中 x1 <= x2 且 y2 >= 0 ，同时对于每个矩形都 必须 满足 x2 - x1 <= w 。

如果一个点在矩形内或者在边上，我们说这个点被矩形覆盖了。

请你在确保每个点都 至少 被一个矩形覆盖的前提下，最少 需要多少个矩形。

注意：一个点可以被多个矩形覆盖。

示例 1：

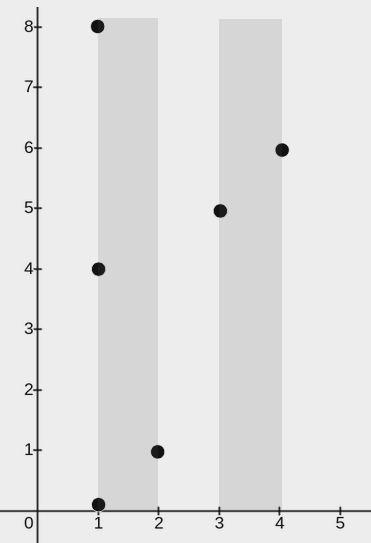
输入：points = [[2,1],[1,0],[1,4],[1,8],[3,5],[4,6]], w = 1
输出：2
解释：
上图展示了一种可行的矩形放置方案：
一个矩形的左下角在 (1, 0) ，右上角在 (2, 8) 。
一个矩形的左下角在 (3, 0) ，右上角在 (4, 8) 。

示例 2：

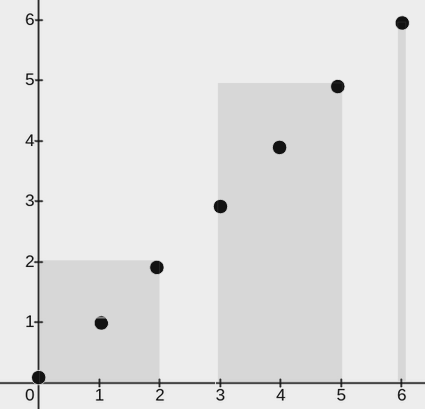
输入：points = [[0,0],[1,1],[2,2],[3,3],[4,4],[5,5],[6,6]], w = 2
输出：3
解释：
上图展示了一种可行的矩形放置方案：
一个矩形的左下角在 (0, 0) ，右上角在 (2, 2) 。
一个矩形的左下角在 (3, 0) ，右上角在 (5, 5) 。
一个矩形的左下角在 (6, 0) ，右上角在 (6, 6) 。

示例 3：

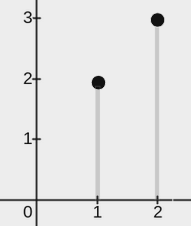
输入：points = [[2,3],[1,2]], w = 0
输出：2
解释：
上图展示了一种可行的矩形放置方案：
一个矩形的左下角在 (1, 0) ，右上角在 (1, 2) 。
一个矩形的左下角在 (2, 0) ，右上角在 (2, 3) 。

说明：

• 1 <= points.length <= 10^5
• points[i].length == 2
• 0 <= xi == points[i][0] <= 10^9
• 0 <= yi == points[i][1] <= 10^9
• 0 <= w <= 10^9
• 所有点坐标 (xi, yi) 互不相同。

思路

有一个二维数组表示平面中的点，给定一个整数w表示矩形x方向的最大宽度，矩形的左下角在x坐标轴上某个点，右上角在第一象限某点。问覆盖坐标平面上所有点最少需要多少个矩形，在矩形边上也算被覆盖了。

由于y轴方向没有限制，我们只考虑x轴方向，可以将坐标平面中的点按照x轴坐标大小排序，然后按w宽度分组计数即可。

最快的写法是将二维坐标转成了一维的x坐标，排序只需要寻址一次。

代码

/**
 * @date 2024-07-31 9:12
 */
public class MinRectanglesToCoverPoints3111 {

    public int minRectanglesToCoverPoints_v1(int[][] points, int w) {
        int n = points.length;
        int[] x = new int[n];
        for (int i = 0; i < n; i++) {
            x[i] = points[i][0];
        }
        Arrays.sort(x);
        int res = 0;
        int r = -1;
        for (int i = 0; i < n; i++) {
            if (x[i] > r) {
                res++;
                r = x[i] + w;
            }
        }
        return res;
    }

    public int minRectanglesToCoverPoints(int[][] points, int w) {
        Arrays.sort(points, (a, b) -> a[0] - b[0]);
        int n = points.length;
        int res = 0;
        int l = 0;
        for (int i = 1; i < n; i++) {
            if (points[i][0] - points[l][0] > w) {
                res++;
                l = i;
            }
        }
        // res 计数的是之前的矩形个数，+1表示将最后的矩形计入
        return res + 1;
    }
}

性能