目标
给你一个下标从 1 开始、大小为 m x n 的整数矩阵 mat,你可以选择任一单元格作为 起始单元格 。
从起始单元格出发,你可以移动到 同一行或同一列 中的任何其他单元格,但前提是目标单元格的值 严格大于 当前单元格的值。
你可以多次重复这一过程,从一个单元格移动到另一个单元格,直到无法再进行任何移动。
请你找出从某个单元开始访问矩阵所能访问的 单元格的最大数量 。
返回一个表示可访问单元格最大数量的整数。
示例 1:
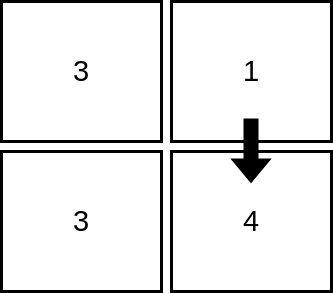
输入:mat = [[3,1],[3,4]]
输出:2
解释:上图展示了从第 1 行、第 2 列的单元格开始,可以访问 2 个单元格。可以证明,无论从哪个单元格开始,最多只能访问 2 个单元格,因此答案是 2 。示例 2:
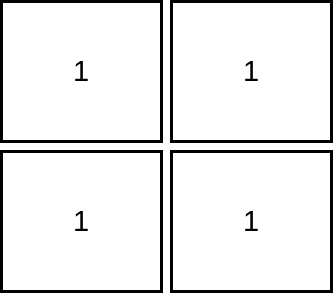
输入:mat = [[1,1],[1,1]]
输出:1
解释:由于目标单元格必须严格大于当前单元格,在本示例中只能访问 1 个单元格。 示例 3:
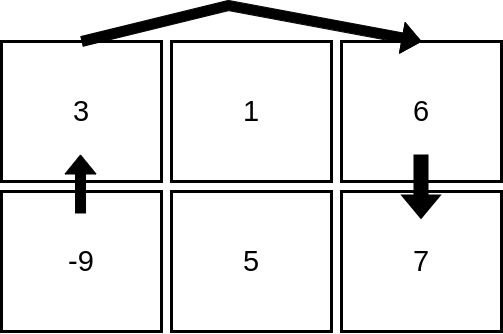
输入:mat = [[3,1,6],[-9,5,7]]
输出:4
解释:上图展示了从第 2 行、第 1 列的单元格开始,可以访问 4 个单元格。可以证明,无论从哪个单元格开始,最多只能访问 4 个单元格,因此答案是 4 。 说明:
- m == mat.length
- n == mat[i].length
- 1 <= m, n <= 10^5
- 1 <= m * n <= 10^5
-10^5 <= mat[i][j] <= 10^5
思路
有一个二维矩阵,我们可以从任意元素出发到达同行或同列的任意严格大于该元素值的位置,问我们最多能访问到多少单元格。
最直接的想法就是建立一个有向无环图,然后求最大路径长度。但是建图的过程需要循环mn(m+n)次,针对每个元素判断其同行同列上严格大于的元素。显然会超时。
于是考虑使用记忆化搜索,结果测试用例 558/566 超时,这个二维数组只有一行,有 100000列,从 1~100000,我在本地测试的时候报栈溢出。
我想要将其转为迭代的形式,但是时间紧迫,简单起见对一行或一列的情况做了特殊处理,排序后去重,最后勉强通过了。
官网题解使用的是动态规划,有时间详细看一下。//todo
代码
/**
* @date 2024-06-19 16:28
*/
public class MaxIncreasingCells2713 {
public int maxIncreasingCells(int[][] mat) {
int res = 0;
int m = mat.length;
int n = mat[0].length;
if (m == 1) {
res = n;
Arrays.sort(mat[0]);
for (int i = 1; i < n; i++) {
if (mat[0][i] == mat[0][i - 1]) {
res--;
}
}
return res;
} else if (n == 1) {
res = m;
Arrays.sort(mat, (a, b) -> a[0] - b[0]);
for (int i = 1; i < m; i++) {
if (mat[i][0] == mat[i - 1][0]) {
res--;
}
}
return res;
}
int l = m * n;
// 将二维坐标映射到一维,dp记录的是从该点为起点的能移动的最大次数
int[] dp = new int[l];
Arrays.fill(dp, -1);
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
res = Math.max(res, move(mat, mat[i][j], i * n + j, i, j, dp));
}
}
return res;
}
public int move(int[][] mat, int curVal, int next, int i, int j, int[] dp) {
int m = mat.length;
int n = mat[0].length;
if (dp[next] > -1) {
return dp[next];
} else if (dp[next] == -2) {
return 1;
}
boolean noNext = true;
for (int k = 0; k < n; k++) {
if (mat[i][k] > curVal) {
noNext = false;
dp[next] = Math.max(dp[next], move(mat, mat[i][k], i * n + k, i, k, dp) + 1);
}
}
for (int k = 0; k < m; k++) {
if (mat[k][j] > curVal) {
noNext = false;
dp[next] = Math.max(dp[next], move(mat, mat[k][j], k * n + j, k, j, dp) + 1);
}
}
if (noNext) {
dp[next] = -2;
return 1;
}
return dp[next];
}
}
性能
