3067.在带权树网络中统计可连接服务器对数目

目标

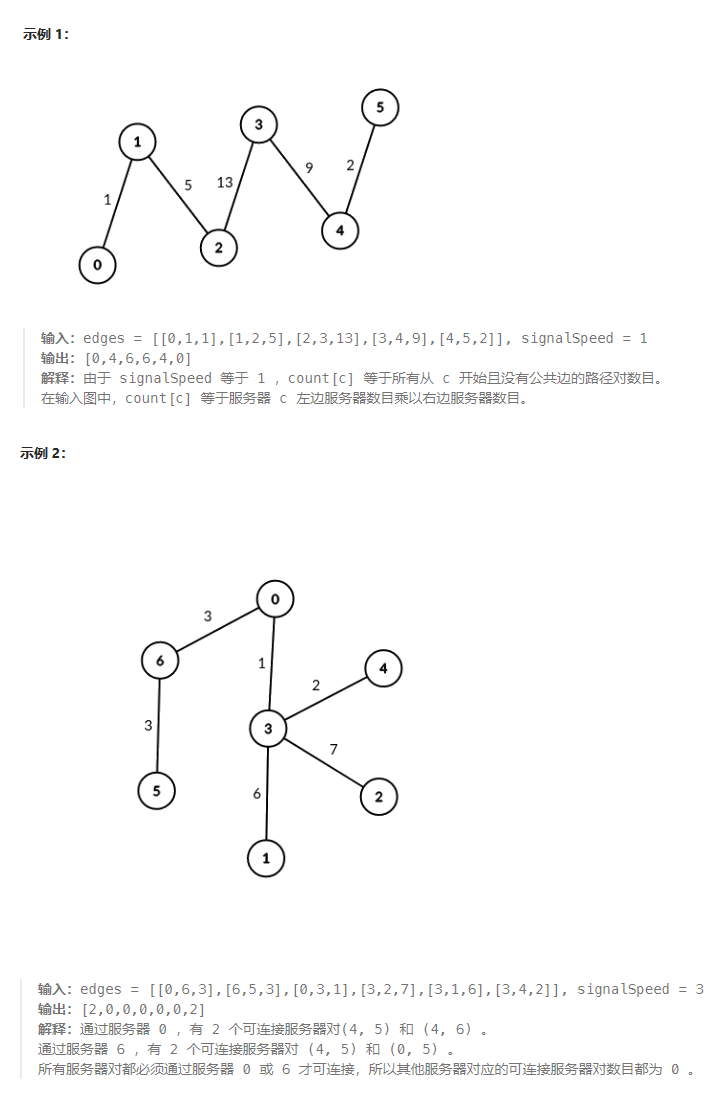
给你一棵无根带权树，树中总共有 n 个节点，分别表示 n 个服务器，服务器从 0 到 n - 1 编号。同时给你一个数组 edges ，其中 edges[i] = [ai, bi, weighti] 表示节点 ai 和 bi 之间有一条双向边，边的权值为 weighti 。再给你一个整数 signalSpeed 。

如果两个服务器 a ，b 和 c 满足以下条件，那么我们称服务器 a 和 b 是通过服务器 c 可连接的 ：

• a < b ，a != c 且 b != c 。
• 从 c 到 a 的距离是可以被 signalSpeed 整除的。
• 从 c 到 b 的距离是可以被 signalSpeed 整除的。
• 从 c 到 b 的路径与从 c 到 a 的路径没有任何公共边。

请你返回一个长度为 n 的整数数组 count ，其中 count[i] 表示通过服务器 i 可连接 的服务器对的 数目 。

说明：

• 2 <= n <= 1000
• edges.length == n - 1
• edges[i].length == 3
• 0 <= ai, bi < n
• edges[i] = [ai, bi, weighti]
• 1 <= weighti <= 10^6
• 1 <= signalSpeed <= 10^6
• 输入保证 edges 构成一棵合法的树。

思路

有一颗无根带权树，所有到服务器 c 的路径，如果路径长度能够被 signalSpeed 整除，并且路径没有重合，则这些服务器可以通过 c 连接。即 c 的每个分支上满足条件的节点可以与其它分支满足条件的节点连接。

遍历每一个节点，以其为根，使用dfs分别计算各分支满足条件的节点，然后计算服务器对。

假设根节点R有4个分支，每个分支上满足条件的节点个数为 a、b、c、d，我们可以使用下面两个方法计算服务器对：

for：
    a：ab + ac + ad
    b：bc + bd
    c：cd

或者

for
    a：0 * a
    b：a * b
    c：(a+b) * c
    d：(a+b+c) * d

第二种方法计算的其实是第一种方法斜线上的和
    a：ab + ac + ad
          /    /
    b：bc + bd
          /
    c：cd

最快的解法应该是换根dp，但是换根后节点数如何变化，处理起来比较复杂，考虑的情况也更多，容易出错。

代码

/**
 * @date 2024-06-04 8:41
 */
public class CountPairsOfConnectableServers3067 {

    private List<int[]>[] g;
    private int speed;

    public int[] countPairsOfConnectableServers_v1(int[][] edges, int signalSpeed) {
        int n = edges.length;
        g = new List[n + 1];
        speed = signalSpeed;
        int[] res = new int[n + 1];
        for (int i = 0; i <= n; i++) {
            g[i] = new ArrayList<>();
        }
        for (int i = 0; i < n; i++) {
            g[edges[i][0]].add(new int[]{edges[i][1], edges[i][2]});
            g[edges[i][1]].add(new int[]{edges[i][0], edges[i][2]});
        }
        for (int i = 0; i <= n; i++) {
            int pre = 0;
            if (g[i].size() == 1) {
                continue;
            }
            for (int j = 0; j < g[i].size(); j++) {
                int cnt = dfs(g[i].get(j)[0], i, g[i].get(j)[1]);
                res[i] += pre * cnt;
                pre += cnt;
            }
        }
        return res;
    }

    public int dfs(int root, int parent, int path) {
        int cnt = path % speed == 0 ? 1 : 0;
        if (g[root].size() == 1 && parent != -1) {
            return cnt;
        }
        for (int[] child : g[root]) {
            if (child[0] == parent) {
                continue;
            }
            cnt += dfs(child[0], root, path + child[1]);
        }
        return cnt;
    }

}

性能