目标
你有 n 个工作和 m 个工人。给定三个数组: difficulty, profit 和 worker ,其中:
- difficulty[i] 表示第 i 个工作的难度,profit[i] 表示第 i 个工作的收益。
- worker[i] 是第 i 个工人的能力,即该工人只能完成难度小于等于 worker[i] 的工作。
每个工人 最多 只能安排 一个 工作,但是一个工作可以 完成多次 。
- 举个例子,如果 3 个工人都尝试完成一份报酬为 $1 的同样工作,那么总收益为 $3 。如果一个工人不能完成任何工作,他的收益为 $0 。
返回 在把工人分配到工作岗位后,我们所能获得的最大利润 。
示例 1:
输入: difficulty = [2,4,6,8,10], profit = [10,20,30,40,50], worker = [4,5,6,7]
输出: 100
解释: 工人被分配的工作难度是 [4,4,6,6] ,分别获得 [20,20,30,30] 的收益。
示例 2:
输入: difficulty = [85,47,57], profit = [24,66,99], worker = [40,25,25]
输出: 0
说明:
- n == difficulty.length
- n == profit.length
- m == worker.length
- 1 <= n, m <= 10^4
- 1 <= difficulty[i], profit[i], worker[i] <= 10^5
思路
现在有一组任务,其难度与收益分别使用两个数组 difficulty 与 profit 表示,还有一个数组表示一组工人的能力。现在需要给工人分配工作,如果分配的工作难度大于工人的能力则无法获取收益,求把工人分配到岗后能够获得的最大收益。
我们只需为每个工人分配其能力范围内的收益最高的工作即可。需要注意的是,题目中没有说难度越高收益越高,并且相同难度的收益也会不同。
难度与收益是通过下标关联的,并且是无序的。
一个很自然的想法是维护一个难度与最大收益的映射,然后直接根据工人的能力二分查找相应的收益并累加。
那么如何同时对两个相关联的数组进行排序就是解题的关键。这里直接将 difficulty 与 profit 的映射通过 hashmap 保存起来,然后对 difficulty 从小到大排序。遍历排序后的 difficulty 数组,计算小于该难度的最大收益并更新到profit 中。根据工人的能力二分查找 profit 并累加即可。
容易出错的点是忘记处理相同难度收益不同的情况,二分查找结果为-1时表示无法完成任务任务,不应取难度最低的任务。
官网题解使用的是 javafx.util.Pair/awt包的Point/ 二维数组来保存映射关系。后面收益最高工作的计算,先对 worker 从小到大排序,使用双指针一个指向worker,一个指向难度,后面工人只需从前一个工人的难度开找即可,没用二分查找。
代码
/**
* @date 2024-05-17 9:20
*/
public class MaxProfitAssignment826 {
public int maxProfitAssignment(int[] difficulty, int[] profit, int[] worker) {
int res = 0;
int n = difficulty.length;
int m = worker.length;
Map<Integer, Integer> profitMap = new HashMap<>();
for (int i = 0; i < n; i++) {
// 存在难度相同的,取最大的
if (profitMap.get(difficulty[i]) == null) {
profitMap.put(difficulty[i], profit[i]);
} else {
profitMap.put(difficulty[i], Math.max(profitMap.get(difficulty[i]), profit[i]));
}
}
Arrays.sort(difficulty);
// 难度从小到大排,更新对应难度可以获得的最大收益
profit[0] = profitMap.get(difficulty[0]);
for (int i = 1; i < n; i++) {
profit[i] = Math.max(profit[i - 1], profitMap.get(difficulty[i]));
}
for (int i = 0; i < m; i++) {
int index = Arrays.binarySearch(difficulty, worker[i]);
if (index >= 0) {
res += profit[index];
} else {
index = -index - 2;
if (index >= 0) {
// 说明没有能力完成
res += profit[index];
}
}
}
return res;
}
// 参考官网题解的答案
public static class Point{
public int x;
public int y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
}
public int maxProfitAssignment_v1(int[] difficulty, int[] profit, int[] worker) {
int res = 0;
int n = difficulty.length;
Point[] jobs = new Point[n];
for (int i = 0; i < n; i++) {
jobs[i] = new Point(difficulty[i], profit[i]);
}
Arrays.sort(jobs, (a, b) -> a.x - b.x);
// 根据工人技能排序
// 越往后能力越高,可以直接接着上一次难度位置向后遍历
Arrays.sort(worker);
int index = 0;
int best = 0;
for (int capability : worker) {
while (index < n && capability >= jobs[index].x) {
best = Math.max(best, jobs[index++].y);
}
res += best;
}
return res;
}
}
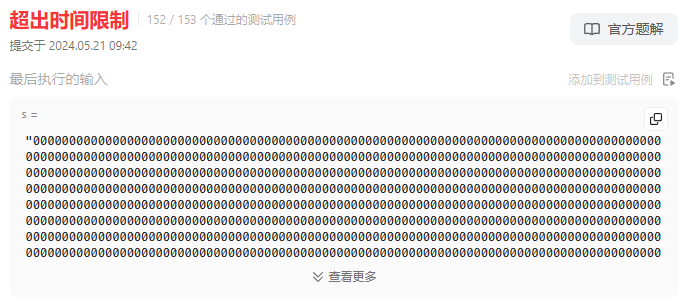
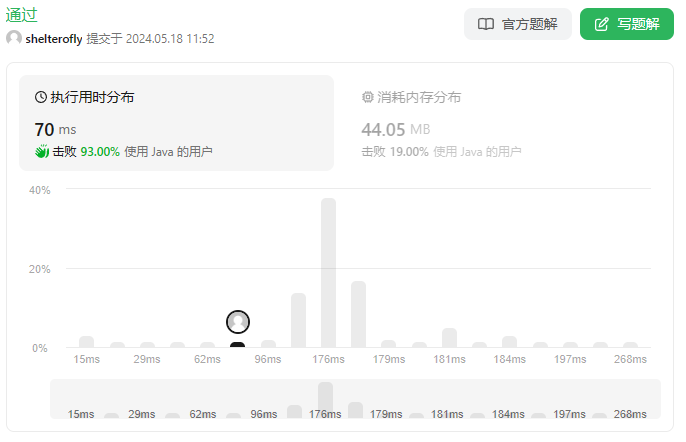
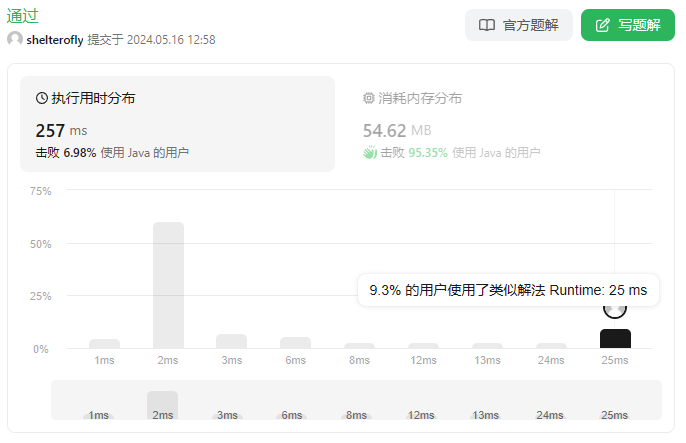
性能
最后计算最大收益时在循环中使用二分查找,时间复杂度为O(mlogn),而使用双指针 difficulty 最多遍历一遍,时间复杂度是O(m + n)应该更快一点。另外使用hashMap效率不高,因为需要计算hashcode,不如直接访问。
改进后