目标
给你两个下标从 0 开始的整数数组 nums 和 divisors 。
divisors[i] 的 可整除性得分 等于满足 nums[j] 能被 divisors[i] 整除的下标 j 的数量。
返回 可整除性得分 最大的整数 divisors[i] 。如果有多个整数具有最大得分,则返回数值最小的一个。
示例 1:
输入:nums = [4,7,9,3,9], divisors = [5,2,3]
输出:3
解释:divisors 中每个元素的可整除性得分为:
divisors[0] 的可整除性得分为 0 ,因为 nums 中没有任何数字能被 5 整除。
divisors[1] 的可整除性得分为 1 ,因为 nums[0] 能被 2 整除。
divisors[2] 的可整除性得分为 3 ,因为 nums[2]、nums[3] 和 nums[4] 都能被 3 整除。
因此,返回 divisors[2] ,它的可整除性得分最大。示例 2:
输入:nums = [20,14,21,10], divisors = [5,7,5]
输出:5
解释:divisors 中每个元素的可整除性得分为:
divisors[0] 的可整除性得分为 2 ,因为 nums[0] 和 nums[3] 都能被 5 整除。
divisors[1] 的可整除性得分为 2 ,因为 nums[1] 和 nums[2] 都能被 7 整除。
divisors[2] 的可整除性得分为 2 ,因为 nums[0] 和 nums[3] 都能被5整除。
由于 divisors[0]、divisors[1] 和 divisors[2] 的可整除性得分都是最大的,因此,我们返回数值最小的一个,即 divisors[2] 。示例 3:
输入:nums = [12], divisors = [10,16]
输出:10
解释:divisors 中每个元素的可整除性得分为:
divisors[0] 的可整除性得分为 0 ,因为 nums 中没有任何数字能被 10 整除。
divisors[1] 的可整除性得分为 0 ,因为 nums 中没有任何数字能被 16 整除。
由于 divisors[0] 和 divisors[1] 的可整除性得分都是最大的,因此,我们返回数值最小的一个,即 divisors[0] 。说明:
- 1 <= nums.length, divisors.length <= 1000
- 1 <= nums[i], divisors[i] <= 10^9
思路
给定一个被除数数组 nums 与除数数组 divisors,nums 中能够被 divisors 整除的元素个数称为相应除数的分数,求分数最大的除数 divisor,如果分数相同则取最小的。
通俗的讲就是找到能够被更多的元素整除的除数,如果有多个则取最小的。
简单题直接放入优先队列即可,但排序其实是没必要的,可以直接在循环中记录结果。
网友还提供了一种算法,不用对每一个 nums 中的元素进行mod运算,而是将 nums 记录到map中,value是其重复次数,同时求出 nums 的最大值。在循环除数的时候,只需要判断 i * divisor 是否在map中即可,结束条件是小于等于最大值。但是这种算法太有针对性,对于那种最大值很大而除数很小的情况可能会超时。
也有网友提供了排序加优化的算法,更通用一些。
代码
/**
* @date 2024-05-18 10:10
*/
public class MaxDivScore2644 {
/**
* 网友的解法 排序加优化 70ms
*/
public int maxDivScore_v3(int[] nums, int[] divisors) {
Arrays.sort(nums);
int n = nums.length;
int dup = 0;
for (int i = 1; i < n; i++) {
if (nums[i] == nums[i - 1]) {
dup++;
}
}
Arrays.sort(divisors);
int ans = 0;
int maxCnt = -1;
for (int d : divisors) {
// 提前结束说明 d 的倍数 d,2d,3d,⋯ ,(maxCnt−dup+1)⋅d 中的最大值已经超出了 nums 的最大值,
// 即使把 nums 中的重复元素也算上,我们也无法统计出比 maxCnt 还多的倍数。
if (maxCnt - dup >= nums[n - 1] / d) {
break;
}
int cnt = 0;
for (int i = n - 1; i >= 0; i--) {
int x = nums[i];
if (x < d) {
break;
}
if (x % d == 0) {
cnt++;
}
}
if (cnt > maxCnt) {
maxCnt = cnt;
ans = d;
}
}
return ans;
}
/**
* 25ms
*/
public int maxDivScore_v1(int[] nums, int[] divisors) {
Map<Integer, Integer> cntMap = new HashMap<>();
int maxNum = 0;
for (int num : nums) {
cntMap.put(num, cntMap.getOrDefault(num, 0) + 1);
maxNum = Math.max(maxNum, num);
}
// 出错点:这里maxCnt的初值为-1,如果为0会跳过无法整除的情况,进入不到if条件里,res还是初值0,而非dividsor
int res = 0, maxCnt = -1;
for (int divisor : divisors) {
int cnt = 0;
int num = divisor;
for (int i = 2; num <= maxNum; i++) {
if (cntMap.containsKey(num)) {
cnt += cntMap.get(num);
}
num = i * divisor;
}
if (cnt > maxCnt || (cnt == maxCnt && res > divisor)) {
maxCnt = cnt;
res = divisor;
}
}
return res;
}
/**
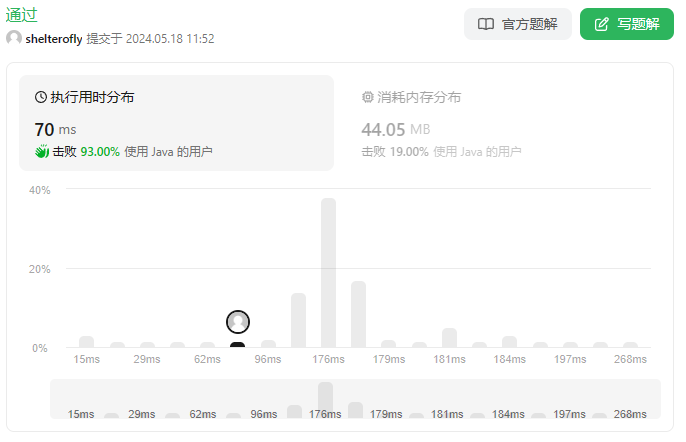
* 使用优先队列 180ms
*/
public int maxDivScore(int[] nums, int[] divisors) {
PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> {
int c = b[1] - a[1];
return c == 0 ? a[0] - b[0] : c;
});
for (int divisor : divisors) {
int cnt = 0;
for (int num : nums) {
if (num % divisor == 0) {
cnt++;
}
}
q.offer(new int[]{divisor, cnt});
}
return q.poll()[0];
}
}
性能
使用优先队列
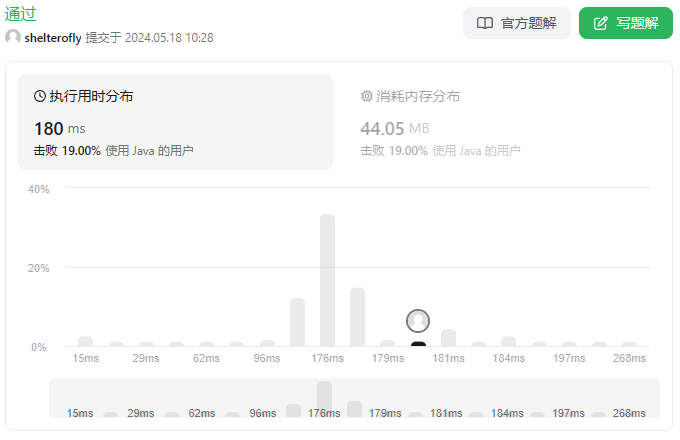
不使用排序,使用hashmap保存nums,成倍增加除数,当除数很大的时候可以跳过一些循环。
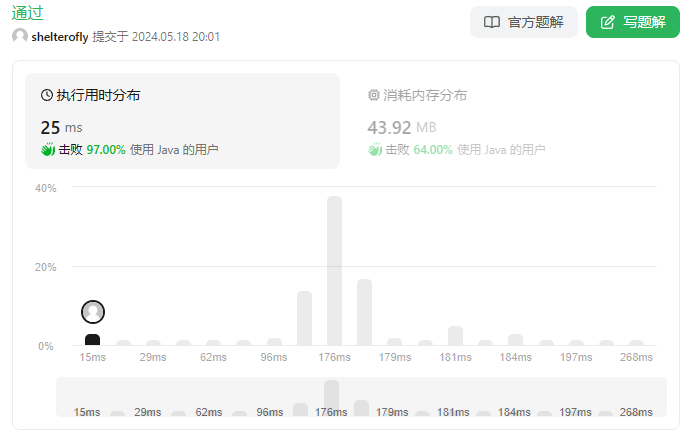
但还是取决于测试用例,如果nums数组没有几个元素,而max又很大,循环次数并不会减少,反而会增加。
例如这个测试用例,上面的方法直接超出限制
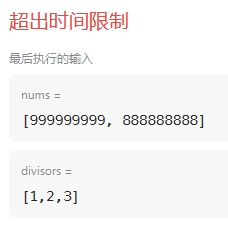
排序加优化: