目标
给你 n 个项目,编号从 0 到 n - 1 。同时给你一个整数数组 milestones ,其中每个 milestones[i] 表示第 i 个项目中的阶段任务数量。
你可以按下面两个规则参与项目中的工作:
- 每周,你将会完成 某一个 项目中的 恰好一个 阶段任务。你每周都 必须 工作。
- 在 连续的 两周中,你 不能 参与并完成同一个项目中的两个阶段任务。
一旦所有项目中的全部阶段任务都完成,或者仅剩余一个阶段任务都会导致你违反上面的规则,那么你将 停止工作 。注意,由于这些条件的限制,你可能无法完成所有阶段任务。
返回在不违反上面规则的情况下你 最多 能工作多少周。
示例 1:
输入:milestones = [1,2,3]
输出:6
解释:一种可能的情形是:
- 第 1 周,你参与并完成项目 0 中的一个阶段任务。
- 第 2 周,你参与并完成项目 2 中的一个阶段任务。
- 第 3 周,你参与并完成项目 1 中的一个阶段任务。
- 第 4 周,你参与并完成项目 2 中的一个阶段任务。
- 第 5 周,你参与并完成项目 1 中的一个阶段任务。
- 第 6 周,你参与并完成项目 2 中的一个阶段任务。
总周数是 6 。
示例 2:
输入:milestones = [5,2,1]
输出:7
解释:一种可能的情形是:
- 第 1 周,你参与并完成项目 0 中的一个阶段任务。
- 第 2 周,你参与并完成项目 1 中的一个阶段任务。
- 第 3 周,你参与并完成项目 0 中的一个阶段任务。
- 第 4 周,你参与并完成项目 1 中的一个阶段任务。
- 第 5 周,你参与并完成项目 0 中的一个阶段任务。
- 第 6 周,你参与并完成项目 2 中的一个阶段任务。
- 第 7 周,你参与并完成项目 0 中的一个阶段任务。
总周数是 7 。
注意,你不能在第 8 周参与完成项目 0 中的最后一个阶段任务,因为这会违反规则。
因此,项目 0 中会有一个阶段任务维持未完成状态。
说明:
- n == milestones.length
- 1 <= n <= 10^5
- 1 <= milestones[i] <= 10^9
思路
给定一个数组,其元素值表示项目的任务数,每一周可以完成任一项目的一个任务,不能连续两周完成同一项目的任务,即每完成一个任务必须切换项目,问最多能完成多少任务。
观察上面的示例发现不能优先选择任务数少的项目,因为任务少的项目先完成后,任务多的项目可能由于没有项目切换被剩下。
刚开始的想法就是先从小到大排序,将个项目的任务数放入优先队列,然后每次从最大与次最大的项目中选取任务,提交之后提示超时。
然后想到没必要一次只减1,于是就直接从最大中减去次最大 next,然后累加 2 * next,提交之后发现对于max == next 时会给出错误答案,于是就记录最大值相同的个数 times,后面累加next * (times + 1) 即可。提交之后发现下面的案例给出的答案不对:
正确的处理过程可以是每次取最大与次最大:
| task1:8 | task2:6 | task3:4 | cost |
|---|---|---|---|
| 7 | 5(end) | 4 | 2 |
| 6 | 4(end) | 4 | 2 |
| 5 | 3(end) | 4 | 2 |
| 4 | 3 | 3(end) | 2 |
| 3 | 2(end) | 3 | 2 |
| 2 | 2 | 2(end) | 2 |
| 1 | 1 | 1(end) | 3 |
| 0 | 0 | 0(end) | 3 |
| - | - | - | 合计:18 |
而提交的算法是这样处理的,违背了上面的处理原则。
| task1:8 | task2:6 | task3:4 | cost |
|---|---|---|---|
| 2 | 0(end) | 4 | 12 |
| 0(end) | 0 | 2 | 4 |
| 0 | 0 | 1 | 1 |
| - | - | - | 合计:17 |
如果考虑第三大元素 third,一次性只减到 third,累加 2 * (next - third) 的话,后续还是要一个一个算。
| task1:8 | task2:6 | task3:4 | cost |
|---|---|---|---|
| 6 | 4(end) | 4 | 2 |
| 5 | 3(end) | 4 | 2 |
| 4 | 3 | 3(end) | 2 |
| 3 | 2(end) | 3 | 2 |
| 2 | 2 | 2(end) | 2 |
| 1 | 1 | 1(end) | 3 |
| 0 | 0 | 0(end) | 3 |
| - | - | - | 合计:18 |
然后还发现对于某些例子是能够计算出正确结果的,例如
| task1:5 | task2:2 | task3:1 | cost |
|---|---|---|---|
| 3 | 0(end) | 1 | 4 |
| 2 | 0 | 0(end) | 2 |
| 1(end) | 0 | 0 | 1 |
| - | - | - | 合计:7 |
于是发现,只要除了最大值其余元素和只要大于等于最大值就可以全部完成。
贪心算法难想,难证明,大多凭直觉,没有通用性。我没有想到这个结论竟然可以推广到多个元素的情况。感觉有点像脑筋急转弯,想通了就很简单。
考虑下面的例子:
最大值每减1,后面的元素都可以同步的减1。
8 8 8 8 8
7 7 7 7 7
......
0 0 0 0 0
----------------
这个就不能同步减了,否则最大值消不完
8 4 3 2 1
7 3 3 2 1
6 2 3 2 1
5 2 2 2 1
4 1 2 2 1
3 1 1 2 1
2 1 1 1 1
1 1 1 1 0
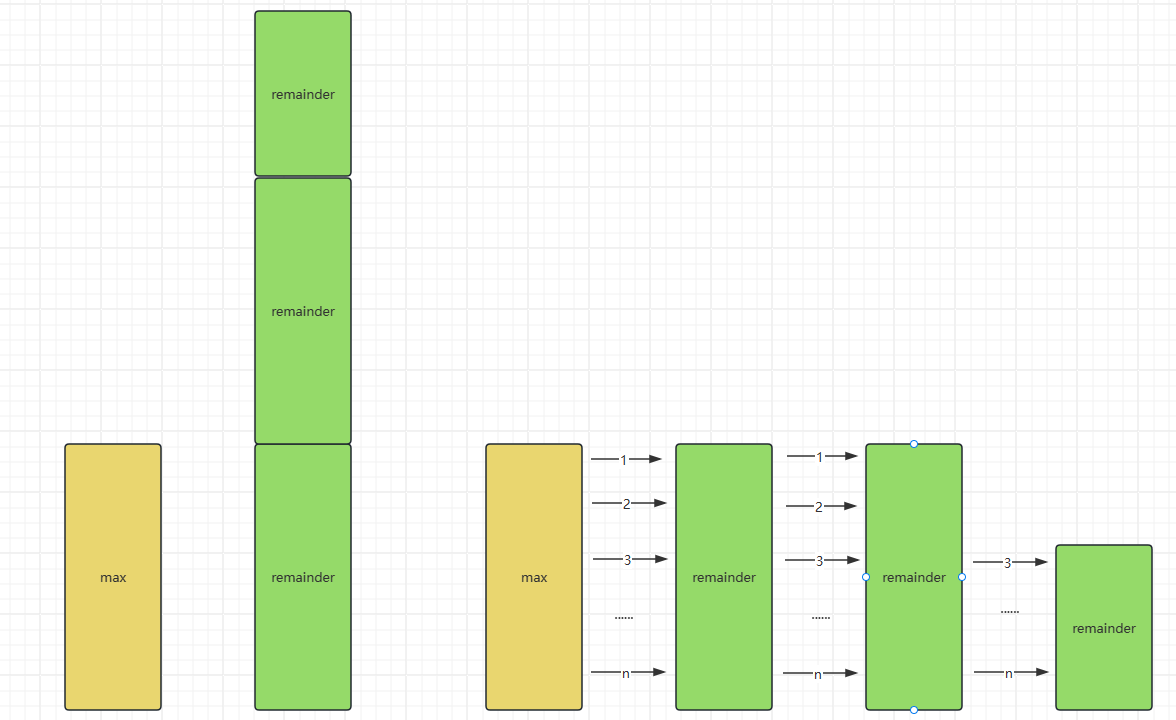
0 0 0 0 0可以想象成两个柱子,最大的是一个柱子,其余的垒成一个柱子,如果大于最大的柱子就截断,作为新的柱子如果还大接着截,不能超过最大的柱子。极端的情况就是全相同,可以全部完成。只要保证有一个柱子与最大的柱子一样高就可以来回切换来完成全部任务。而如果其余的柱子垒起来没有最大的高,那么只能完成 其余之和*2+1
代码
package medium;
/**
* @date 2024-05-16 8:37
*/
public class NumberOfWeeks1953 {
/**
* 执行通过
* 如果最大的小于等于其余之和,那么所有任务均可完成
* 如果最大的大于其余之和,那么可以完成其余之和*2+1
*/
public long numberOfWeeks_v2(int[] milestones) {
long sum = 0;
int max = 0;
for (int milestone : milestones) {
if (milestone > max) {
max = milestone;
}
sum += milestone;
}
long remainder = sum - max;
return remainder < max ? remainder * 2 + 1 : sum;
}
/**
* 这个算法是调试出来的
*/
public long numberOfWeeks_v1(int[] milestones) {
long res = 0;
PriorityQueue<Integer> q = new PriorityQueue<>(Comparator.reverseOrder());
for (int milestone : milestones) {
q.offer(milestone);
}
while (!q.isEmpty()) {
int head = q.poll();
// 输入数组中的值均大于0,res放在这里加,以免漏掉最后一个
res++;
if (q.isEmpty()) {
// 如果后面没有任务,连续两周完成同一项目的任务会违反规则,直接返回
return res;
}
int next = q.poll();
int times = 1;
while (!q.isEmpty() && next == head) {
times++;
next = q.poll();
}
if (q.size() == 1 && q.peek() + next > head) {
// 处理最后三个,如果其余两个大于最大值就返回它们的和,减1是因为为了防止漏掉最后一个加了1
return res + head * times + next + q.poll() - 1;
}
res += (long) next * (times + 1) - 1;
head -= next;
if (head > 0) {
for (int i = 0; i < times; i++) {
q.offer(head);
}
}
}
return res;
}
性能
方法一
方法二