目标
给定一个由 n 个节点组成的网络,用 n x n 个邻接矩阵 graph 表示。在节点网络中,只有当 graph[i][j] = 1 时,节点 i 能够直接连接到另一个节点 j。
一些节点 initial 最初被恶意软件感染。只要两个节点直接连接,且其中至少一个节点受到恶意软件的感染,那么两个节点都将被恶意软件感染。这种恶意软件的传播将继续,直到没有更多的节点可以被这种方式感染。
假设 M(initial) 是在恶意软件停止传播之后,整个网络中感染恶意软件的最终节点数。
我们可以从 initial 中删除一个节点,并完全移除该节点以及从该节点到任何其他节点的任何连接。
请返回移除后能够使 M(initial) 最小化的节点。如果有多个节点满足条件,返回索引 最小的节点 。
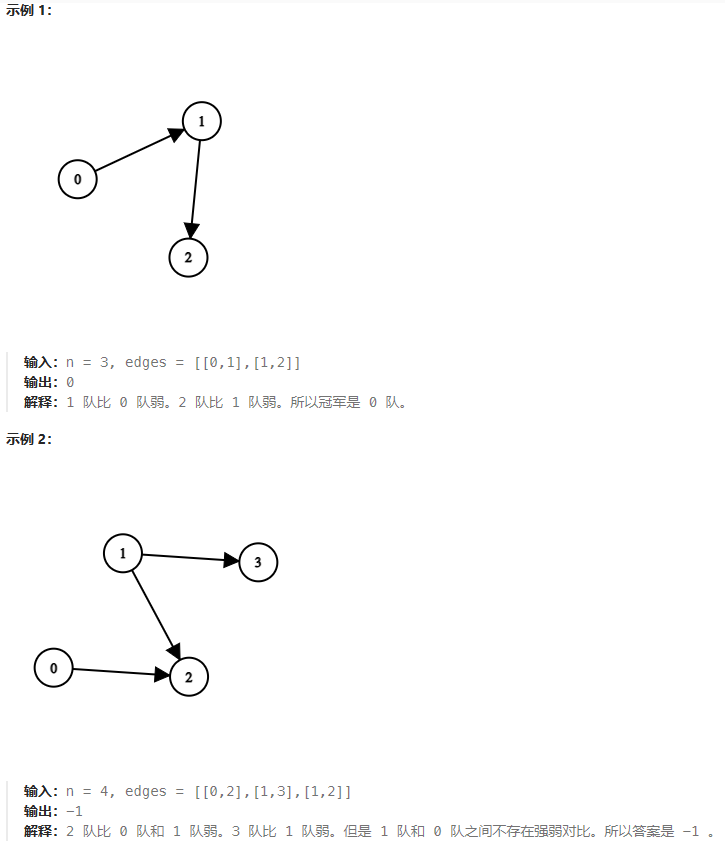
示例 1:
输入:graph = [[1,1,0],[1,1,0],[0,0,1]], initial = [0,1]
输出:0
示例 2:
输入:graph = [[1,1,0],[1,1,1],[0,1,1]], initial = [0,1]
输出:1
示例 3:
输入:graph = [[1,1,0,0],[1,1,1,0],[0,1,1,1],[0,0,1,1]], initial = [0,1]
输出:1
说明:
- n == graph.length
- n == graph[i].length
- 2 <= n <= 300
graph[i][j] 是 0 或 1.graph[i][j] == graph[j][i]graph[i][i] == 1- 1 <= initial.length < n
- 0 <= initial[i] <= n - 1
- initial 中每个整数都不同
思路
这个和昨天的题的区别是移除节点之后原来连通的区域可能就断开了。刚开始想,昨天的需要排除掉同一连通区域存在多个感染节点的情况,今天这个就不能排除了。但是其影响的节点数也不能通过连通区域节点个数来计算。处理起来就比较复杂了,不能简单地根据直接相连的节点数来判断。当连通区域中含有多个感染节点时,需要区分边缘感染节点与中间感染节点,边缘感染节点又与孤立的感染节点相同,都是减少1。然后还要考虑连通区域仅有一个感染节点的情况。
区分 单一边缘感染节点 与 孤立感染节点
2、3 感染,返回3
0 - 1
|
3
2
无需区分 多个边缘感染节点 与 孤立感染节点
1、2、3 感染,返回1
0 - 1
|
3
2
区分 中间感染节点 与 孤立感染节点,并且不能仅根据直接相连的非感染节点来判断
0 、2、4、8 感染,返回8
7
| \
0 4 - 6
|
1 - 8 - 3
|
2 5
错了好多次,终于调试过了。正面确实不太好求解。总结一下就是:
- 连通区域存在多个感染节点
- 去掉边缘的感染节点,感染节点总数减少1,全是边缘感染节点与包含中间感染节点是一样的
- 去掉非边缘感染节点,需要dfs获取不含感染节点路径的节点总数
- 连通区域仅有1个感染节点(可以是孤立感染节点、边缘节点、中间节点)
最终答案需要获取以上减少最多的节点,如果存在多个,返回下标最小的。
代码里是按边缘感染节点与中间感染节点分的:
- 边缘感染节点
- 孤立感染节点,减1
- 连通区域内有多个边缘感染节点,减1
- 连通区域内仅有一个边缘感染节点,减连通区域节点个数
- 中间感染节点(如果存在中间节点就不考虑边缘节点了,因为题目中限制了1 <= initial.length < n,一定存在可以减少2个的中间节点,分析到这里时我以为我发现了官网的漏洞,错误的实现也能通过,想要贡献测试用例呢,结果提示测试用例非有效值。如果是小于等于n这个解法就得多一个判断条件initial.length == n,直接取最小下标)
- 仅有一个中间感染节点,连通区域节点个数
- 有多个中间感染节点,dfs搜索不含感染节点路径上的非感染节点个数,如果有感染节点,那么它也是减1,不过这里不再比较了,原因上面也说过了。
代码中d存的是中间节点(包括指向自身的边大于2),如果d为空则表示连通区域全是边缘感染节点(边为2),或孤立感染节点(边为1)。
对于全是边缘感染节点与孤立感染节点的情况,取下标最小即可。而对于中间感染节点,通过dfs来查找连通个数。如果通过dfs查找的个数为1,并且它还是中间感染节点,那么它周围全是感染节点。按道理来说,应该与边缘节点一起取最小下标。但是题目给出了限制,那么一定存在一个可以减少2的中间节点。
通过上面的分析只是说明了该问题正向分析的复杂性,如果不是不断尝试,很难直接把上面的所有情况想清楚。所以,上面的分析也没有太大的用处,过一段时间重做这个题,还是会踩坑。
官网题解使用的是逆向思维,统计的是从每个非感染节点出发不经过感染节点所经历的个数,在dfs过程中使用状态机来标识感染节点的个数。如果只遇到了1个感染节点,那么累加刚才遍历的节点个数,而如果有多个,那么就只能减少它自己。因此,如果存在只遇到一个感染节点的情况,就取个数最大的。否则取下标最小的。
其实,只遇到一个感染节点的情况包括了上面的单一边缘感染节点、中间单一感染节点以及多个中间感染节点(dfs非感染个数不为0的情况,即路径上不含有感染节点)的情况,而遇到多个感染节点,则说明被多个感染节点包围/半包围(对应全是边缘节点、边缘与中间、全中间,后面两种情况上面的算法忽略掉了),并且取最小下标直接包括了孤立感染节点。
可以发现同样是一步处理,我们赋予它不同的内涵,其所应对的场景就大为不同。
代码
/**
* @date 2024-04-17 8:46
*/
public class MinMalwareSpread928 {
public int[] u;
TreeSet<Integer> s;
HashSet<Integer> d = new HashSet<>();
List<Integer>[] g;
public void merge(int x, int y) {
HashSet<Integer> tmp = new HashSet<>();
int rx = find(x, tmp);
int ry = find(y, tmp);
d.addAll(tmp);
if (s.contains(rx) && s.contains(ry)) {
if (rx > ry) {
u[rx] = ry;
} else if (rx < ry) {
u[ry] = rx;
}
} else if (s.contains(ry)) {
u[rx] = ry;
} else {
u[ry] = rx;
}
}
public int find(int x, HashSet<Integer> tmp) {
if (x != u[x]) {
if (s.contains(x) && s.contains(u[x])) {
if (g[x].size() > 2) {
tmp.add(x);
}
if (g[u[x]].size() > 2) {
tmp.add(u[x]);
}
}
x = find(u[x], tmp);
}
return u[x];
}
public int find(int x) {
if (x != u[x]) {
x = find(u[x]);
}
return u[x];
}
public int count(int x) {
int cnt = 0;
int rt = find(x);
for (int i = 0; i < u.length; i++) {
if (rt == find(i)) {
cnt++;
}
}
return cnt;
}
public int countMalware(int x) {
int cnt = 0;
int rt = find(x);
for (int i = 0; i < u.length; i++) {
if (rt == find(i) && s.contains(i)) {
cnt++;
}
}
return cnt;
}
public int adjacencyUninfected(int x, int parent) {
int cnt = 1;
boolean[] visited = new boolean[u.length];
for (Integer node : g[x]) {
if (parent == node || node == x || visited[node]) {
continue;
}
visited = new boolean[u.length];
if (!s.contains(node)) {
int subCnt = dfs(node, x, visited);
if (subCnt != 0) {
cnt += subCnt;
}
}
}
return cnt;
}
public int dfs(int x, int parent, boolean[] visited) {
if (s.contains(x)) {
return 0;
}
int cnt = 1;
for (Integer node : g[x]) {
if (parent == node || node == x || visited[node]) {
visited[node] = true;
continue;
}
visited[node] = true;
if (s.contains(node)) {
return 0;
}
int subCnt = dfs(node, x, visited);
if (subCnt == 0) {
return 0;
} else {
cnt += subCnt;
}
}
return cnt;
}
public int minMalwareSpread(int[][] graph, int[] initial) {
int n = graph.length;
g = new ArrayList[n];
u = new int[n];
for (int i = 0; i < n; i++) {
g[i] = new ArrayList<>(n);
u[i] = i;
}
s = new TreeSet<>();
for (int i : initial) {
s.add(i);
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (graph[i][j] == 1) {
g[i].add(j);
merge(i, j);
}
}
}
int res = Integer.MAX_VALUE;
int tmp = Integer.MAX_VALUE;
TreeSet<Integer> ini = new TreeSet<>((x, y) -> count(y) - count(x) == 0 ? (adjacencyUninfected(y, -1) - adjacencyUninfected(x, -1) == 0 ? x - y : adjacencyUninfected(y, -1) - adjacencyUninfected(x, -1)) : count(y) - count(x));
if (d.isEmpty()) {
// d为空表示连通区域仅有1个感染节点
for (int i : initial) {
if (countMalware(i) == 1 && count(i) > 1) {
// 连通区域节点数大于1
if (tmp == Integer.MAX_VALUE) {
tmp = i;
} else {
int ci = count(i);
int ct = count(tmp);
if (ci > ct) {
// 取连通区域节点数大的
tmp = i;
} else if (ci == ct) {
// 如果相等取下标小的
tmp = Math.min(i, tmp);
}
}
} else {
// 对于孤立节点,直接取索引最小的即可
res = Math.min(i, res);
}
}
// 如果全部是孤立节点,取res,否则取tmp
return tmp == Integer.MAX_VALUE ? res : tmp;
} else {
ini.addAll(d);
}
return ini.first();
}
}
性能