2924.找到冠军II

目标

一场比赛中共有 n 支队伍，按从 0 到 n - 1 编号。每支队伍也是 有向无环图（DAG, Directed Acyclic Graph） 上的一个节点。

给你一个整数 n 和一个下标从 0 开始、长度为 m 的二维整数数组 edges 表示这个有向无环图，其中 edges[i] = [ui, vi] 表示图中存在一条从 ui 队到 vi 队的有向边。

从 a 队到 b 队的有向边意味着 a 队比 b 队 强 ，也就是 b 队比 a 队 弱 。

在这场比赛中，如果不存在某支强于 a 队的队伍，则认为 a 队将会是 冠军 。

如果这场比赛存在 唯一 一个冠军，则返回将会成为冠军的队伍。否则，返回 -1 。

注意：

环 是形如 a1, a2, ..., an, an+1 的一个序列，且满足：节点 a1 与节点 an+1 是同一个节点；节点 a1, a2, ..., an 互不相同；对于范围 [1, n] 中的每个 i ，均存在一条从节点 ai 到节点 ai+1 的有向边。

有向无环图 是不存在任何环的有向图。

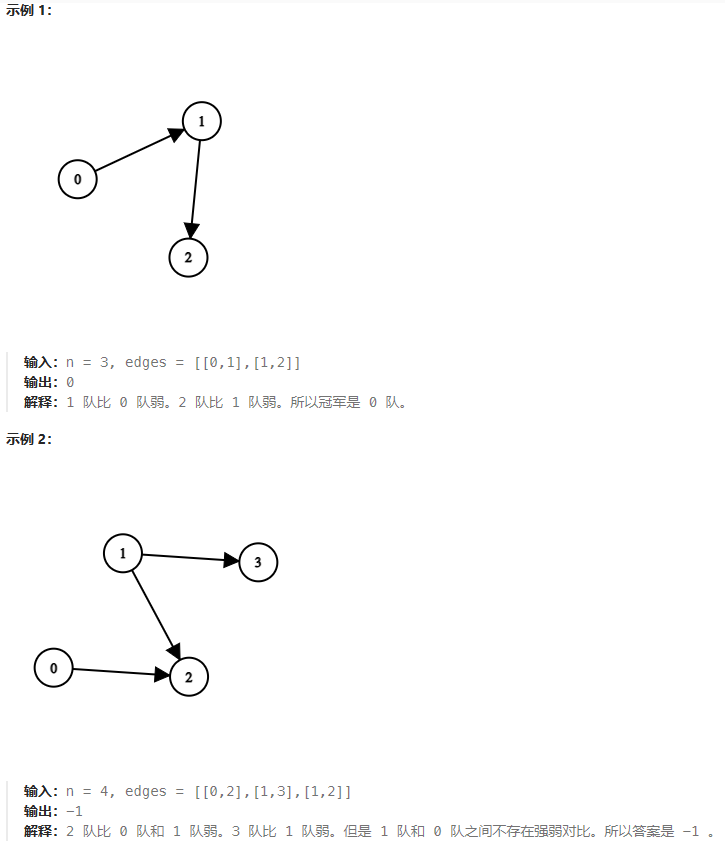
说明：

• 1 <= n <= 100
• m == edges.length
• 0 <= m <= n * (n - 1) / 2
• edges[i].length == 2
• 0 <= edge[i][j] <= n - 1
• edges[i][0] != edges[i][1]
• 生成的输入满足：如果 a 队比 b 队强，就不存在 b 队比 a 队强
• 生成的输入满足：如果 a 队比 b 队强，b 队比 c 队强，那么 a 队比 c 队强

思路

如果只有一个节点，那它就是冠军。入度非0的不是冠军。多个没有强弱关系的的节点，返回-1，例如，n=2，边为空。

只需计算没有被标记为weaker节点的index，如果多于1个返回-1。

代码

/**
 * @date 2024-04-13 19:22
 */
public class FindChampion2924 {
    public int findChampion(int n, int[][] edges) {
        boolean[] weaker = new boolean[n];
        for (int[] edge : edges) {
            weaker[edge[1]] = true;
        }
        int championIndex = -1;
        for (int i = 0; i < weaker.length; i++) {
            if (weaker[i]) {
                continue;
            }
            if (championIndex != -1) {
                return -1;
            }
            championIndex = i;
        }
        return championIndex;
    }
}

性能