目标
给你一棵树,树上有 n 个节点,按从 0 到 n-1 编号。树以父节点数组的形式给出,其中 parent[i] 是节点 i 的父节点。树的根节点是编号为 0 的节点。
树节点的第 k 个祖先节点是从该节点到根节点路径上的第 k 个节点。
实现 TreeAncestor 类:
- TreeAncestor(int n, int[] parent) 对树和父数组中的节点数初始化对象。
- getKthAncestor(int node, int k) 返回节点 node 的第 k 个祖先节点。如果不存在这样的祖先节点,返回 -1 。
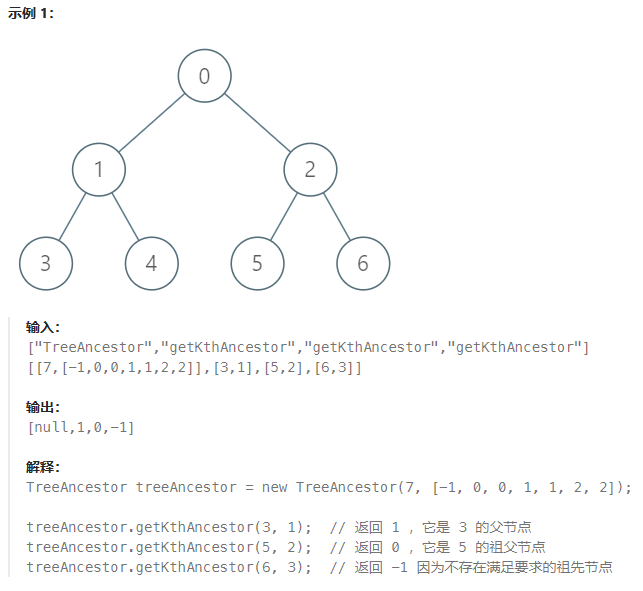
说明:
- 1 <= k <= n <= 5 * 10^4
- parent[0] == -1 表示编号为 0 的节点是根节点。
- 对于所有的 0 < i < n ,0 <= parent[i] < n 总成立
- 0 <= node < n
- 至多查询 5 * 10^4 次
思路
这个题让我们维护一个数据结构,来查找树中任意节点的第k个祖先节点。直接的想法是保存每一个节点的父节点,需要的时候直接根据下标获取。刚开始用的 int[][] 超出了空间限制,后来改成 List<Integer>[] 虽然多通过了几个测试用例,但是后面会超时。仔细分析最坏的情况下(所有节点仅有一个子树的情况),需要添加 n(n+1)/2 个父节点(首项为1,公差为1的等差数列求和),时间复杂度是O(n^2)。
一个解决办法是不要保存重复的父节点,以只有一个子树的情况举例,最后一个节点第k个祖先,就是其父节点的第k-1个祖先。如果这个节点已经保存有祖先节点的信息,就无需重复计算了。
所以我的解决方案就是使用缓存,如果父节点的祖先信息没有保存,就将当前节点的祖先信息写入缓存,直到遇到存在缓存的祖先节点,如果它记录的祖先节点个数大于k - cnt就直接返回,否则继续向该缓存的祖先节点集合添加,直到遇到下一个有缓存的节点或者cnt == k。
这种方法虽然能够通过,但是与测试用例的的顺序是有关的,如果是从子节点逐步向前测试的话,缓存一直不命中,时间复杂度还是O(n^2)。
官方的解法使用的是倍增的思想,好像还挺常用的,算是个模板算法。核心思想是保存当前节点的父节点,爷爷节点,爷爷的爷爷节点......,即每个节点 x 的第 2^i 个祖先节点。这样不论k取什么值,都可以分解为不同的2的幂之和,然后向前查找即可。预处理的时间复杂度是O(nlogn),查询的时间复杂度是O(logk)。
代码
/**
* @date 2024-04-06 9:45
*/
public class TreeAncestor1483 {
/**倍增的写法 */
public static class TreeAncestor_v4 {
int[][] dp;
public TreeAncestor_v4(int n, int[] parent) {
dp = new int[16][];
dp[0] = parent;
for (int i = 1; i < 16; i++) {
dp[i] = new int[n];
Arrays.fill(dp[i], -1);
}
for (int i = 1; i < 16; i++) {
for (int j = 0; j < n; j++) {
if (dp[i - 1][j] != -1) {
dp[i][j] = dp[i - 1][dp[i - 1][j]];
}
}
}
}
public int getKthAncestor(int node, int k) {
int p = node;
int b = 0;
int mod;
while (k != 0) {
mod = k & 1;
if (mod == 1) {
p = dp[b][p];
if (p == -1) {
return -1;
}
}
k = k >> 1;
b++;
}
return p;
}
}
int[] parent;
List<Integer>[] cache;
public TreeAncestor1483(int n, int[] parent) {
this.parent = parent;
cache = new ArrayList[n];
for (int i = 0; i < cache.length; i++) {
cache[i] = new ArrayList<>();
}
}
public int getKthAncestor(int node, int k) {
if (node == -1) {
return -1;
}
int cnt = 0;
int p = node;
while (cnt != k && p != -1) {
if (cache[p].size() == 0) {
cache[node].add(parent[p]);
p = parent[p];
cnt++;
} else {
if (cache[p].size() >= k - cnt) {
return cache[p].get(k - cnt - 1);
} else {
cnt += cache[p].size();
node = p;
p = cache[p].get(cache[p].size() - 1);
}
}
}
return p;
}
}性能
这里是使用缓存写法的耗时,官方题解的耗时差不多也是这个样。
使用倍增的写法