明天五一假期。今天的题太友好了,循环里面判断就行了。
月度归档: 2024 年 4 月
1329.将矩阵按对角线排序
目标
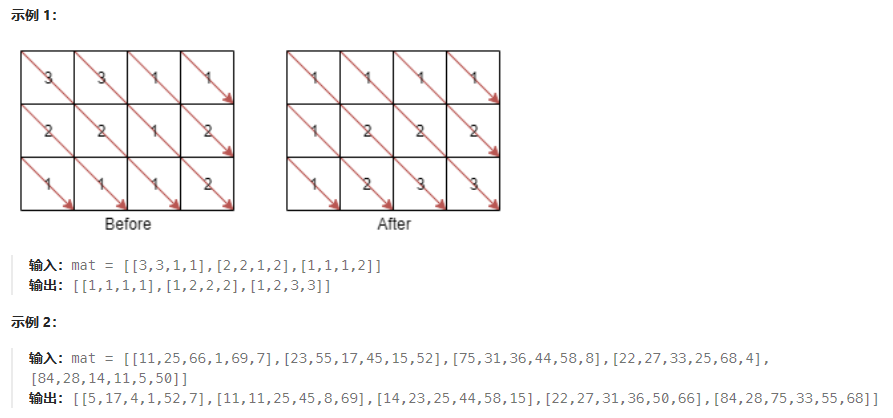
矩阵对角线 是一条从矩阵最上面行或者最左侧列中的某个元素开始的对角线,沿右下方向一直到矩阵末尾的元素。例如,矩阵 mat 有 6 行 3 列,从 mat[2][0] 开始的 矩阵对角线 将会经过 mat[2][0]、mat[3][1] 和 mat[4][2] 。
给你一个 m * n 的整数矩阵 mat ,请你将同一条 矩阵对角线 上的元素按升序排序后,返回排好序的矩阵。
说明:
- m == mat.length
- n == mat[i].length
- 1 <= m, n <= 100
1 <= mat[i][j] <= 100
思路
排序是一大块内容,有机会统一总结一下。// todo
这里偷懒使用了优先队列,先放到队列里面排序,然后再写回去。
代码
/**
* @date 2024-04-29 0:26
*/
public class DiagonalSort1329 {
public int[][] diagonalSort(int[][] mat) {
int m = mat.length;
int n = mat[0].length;
int i;
int j;
PriorityQueue<Integer> q = new PriorityQueue();
for (int col = 0; col < n; col++) {
j = col;
i = 0;
while (i < m && j < n) {
q.offer(mat[i++][j++]);
}
j = col;
i = 0;
while (i < m && j < n) {
mat[i++][j++] = q.poll();
}
}
for (int row = 1; row < m; row++) {
j = 0;
i = row;
while (i < m && j < n) {
q.offer(mat[i++][j++]);
}
j = 0;
i = row;
while (i < m && j < n) {
mat[i++][j++] = q.poll();
}
}
return mat;
}
}
性能
1017.负二进制转换
// todo
2639.查询网格图中每一列的宽度
目标
给你一个下标从 0 开始的 m * n 整数矩阵 grid 。矩阵中某一列的宽度是这一列数字的最大 字符串长度 。
- 比方说,如果 grid = [[-10], [3], [12]] ,那么唯一一列的宽度是 3 ,因为 -10 的字符串长度为 3 。
请你返回一个大小为 n 的整数数组 ans ,其中 ans[i] 是第 i 列的宽度。
一个有 len 个数位的整数 x ,如果是非负数,那么 字符串长度 为 len ,否则为 len + 1 。
示例 1:
输入:grid = [[1],[22],[333]]
输出:[3]
解释:第 0 列中,333 字符串长度为 3 。示例 2:
输入:grid = [[-15,1,3],[15,7,12],[5,6,-2]]
输出:[3,1,2]
解释:
第 0 列中,只有 -15 字符串长度为 3 。
第 1 列中,所有整数的字符串长度都是 1 。
第 2 列中,12 和 -2 的字符串长度都为 2 。
说明:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 100
-10^9 <= grid[r][c] <= 10^9
思路
这个题核心就是如何计算数字的长度。我们可以枚举 9, 99, 999, 9999, 99999, 999999, 9999999, 99999999, 999999999, Integer.MAX_VALUE,分别与这些值比较,Integer.stringSize就是如此实现的。对于负数需要将长度加1 int size = (i < 0) ? stringSize(-i) + 1 : stringSize(i);。
也可以循环除以10直到0来计算长度。一个优化的点是不必求每一个数的长度,只需要求出最大值 max 与 最小值 min的长度即可。网友还提供了一个小技巧可以减少对较小值的长度计算。选取 max/10 和 -min 中的较大值来计算长度 l,取 l+1。解释如下:如果 min > 0 那么 -min < 0,我们取到 max/10 的长度,所以长度为 l+1。如果 min < 0,并且 -min > max/10,我们取到 -min,长度需要加上负号,即 l+1。这里需要解释一下 -min < max && -min > max/10 的情况,这时 max 的长度与 -min 的长度加1 是相同的。而如果 min < 0,且 -min < max/10,取 max/10 长度减小了1,所以取 l+1。
代码
/**
* @date 2024-04-27 18:39
*/
public class FindColumnWidth2639 {
int[] sizeTable = {9, 99, 999, 9999, 99999, 999999, 9999999,
99999999, 999999999, Integer.MAX_VALUE};
int stringSize(int x) {
int j;
if (x < 0) {
x = -x;
j = 2;
} else {
j = 1;
}
for (int i = 0; ; i++) {
if (x <= sizeTable[i]) {
return i + j;
}
}
}
public int[] findColumnWidth(int[][] grid) {
int n = grid[0].length;
int[] res = new int[n];
int[] negative = new int[n];
for (int[] ints : grid) {
for (int i = 0; i < n; i++) {
if (ints[i] < negative[i]) {
negative[i] = ints[i];
} else if (ints[i] > res[i]) {
res[i] = ints[i];
}
}
}
for (int i = 0; i < n; i++) {
res[i] = Math.max(stringSize(res[i]), stringSize(negative[i]));
}
return res;
}
}
性能
1146.快照数组
这个题涉及到hash表与二分查找,发现之前2529.正整数和负整数的最大计数里面寻找上界写错了。
有时间了再整理一下吧。
2739.总行驶距离
目标
卡车有两个油箱。给你两个整数,mainTank 表示主油箱中的燃料(以升为单位),additionalTank 表示副油箱中的燃料(以升为单位)。
该卡车每耗费 1 升燃料都可以行驶 10 km。每当主油箱使用了 5 升燃料时,如果副油箱至少有 1 升燃料,则会将 1 升燃料从副油箱转移到主油箱。
返回卡车可以行驶的最大距离。
注意:从副油箱向主油箱注入燃料不是连续行为。这一事件会在每消耗 5 升燃料时突然且立即发生。
示例 1:
输入:mainTank = 5, additionalTank = 10
输出:60
解释:
在用掉 5 升燃料后,主油箱中燃料还剩下 (5 - 5 + 1) = 1 升,行驶距离为 50km 。
在用掉剩下的 1 升燃料后,没有新的燃料注入到主油箱中,主油箱变为空。
总行驶距离为 60km 。示例 2:
输入:mainTank = 1, additionalTank = 2
输出:10
解释:
在用掉 1 升燃料后,主油箱变为空。
总行驶距离为 10km 。说明:
- 1 <= mainTank, additionalTank <= 100
思路
这里面的关键点在于第一次消耗完5升燃料之后会触发副油箱注入,后面消耗的5升燃料中包含有副油箱注入的1升。即第一次消耗完成后主油箱每消耗4升就会触发燃料注入。
例如主油箱有9L,副油箱有1L,那么总共可以消耗10L燃料。
注入燃料的总次数等于 1 + (mainTank -5)/4 = (mainTank - 1)/4。
代码
/**
* @date 2024-04-25 0:11
*/
public class DistanceTraveled2739 {
public int distanceTraveled_v1(int mainTank, int additionalTank) {
return 10 * (mainTank + Math.min((mainTank - 1) / 4, additionalTank));
}
public int distanceTraveled(int mainTank, int additionalTank) {
int res = 0;
while (mainTank >= 5) {
res += 5;
mainTank -= 5;
if (additionalTank > 0) {
additionalTank--;
mainTank++;
}
}
res += mainTank;
return res * 10;
}
}性能

2385.感染二叉树需要的总时间
目标
给你一棵二叉树的根节点 root ,二叉树中节点的值 互不相同 。另给你一个整数 start 。在第 0 分钟,感染 将会从值为 start 的节点开始爆发。
每分钟,如果节点满足以下全部条件,就会被感染:
- 节点此前还没有感染。
- 节点与一个已感染节点相邻。
返回感染整棵树需要的分钟数。
示例 1:
输入:root = [1,5,3,null,4,10,6,9,2], start = 3
输出:4
解释:节点按以下过程被感染:
- 第 0 分钟:节点 3
- 第 1 分钟:节点 1、10、6
- 第 2 分钟:节点5
- 第 3 分钟:节点 4
- 第 4 分钟:节点 9 和 2
感染整棵树需要 4 分钟,所以返回 4 。示例 2:
输入:root = [1], start = 1
输出:0
解释:第 0 分钟,树中唯一一个节点处于感染状态,返回 0 。说明:
- 树中节点的数目在范围 [1, 10^5] 内
- 1 <= Node.val <= 10^5
- 每个节点的值 互不相同
- 树中必定存在值为 start 的节点
思路
从树中任意节点开始,每过一分钟感染会向周围扩散,问感染整棵树需要多久。
首先我们要找到感染开始的节点。从这个节点出发,向左右子树点以及父节点扩散。可以将树转换为以感染节点为起点的有向无环连通图,这样问题被转换为求起点到图中任意节点的最长路径。
如果不想建图可以考虑扩散的具体路径,刚开始很难把各种情况都考虑到。我们需要计算以开始节点为根的子树高度 h(start),并依次比较开始节点到祖先节点路径长度加上祖先另一子树高度的最大值,即max(d(start) - d(ancestor) + h(anotherAncestorSubtree)),再取二者的最大值即可。特别需要注意的是,不能使用子树高度之差来计算祖先与开始节点的路径长度。例如,E是开始节点,E到B的路径长度为d(E) - d(B) = 2 - 1 = 1,而如果使用子树高度相减的话就得到了h(B) - h(E) = 3 - 0 = 3。
A
/ \
B C
/ \
D E
|
F
|
G在具体实现的时候如何判断祖先节点的哪个子树包含开始节点困扰了我半天。刚开始我选择了一个标志位,分别在左右子树递归结束的时候检测该标志,发现找到之后立即重置该标志,这样父节点就知道了是左子树还是右子树包含开始节点。但问题是再向上返回的时候就无法判断了。
可以考虑返回二维数组,也有网友的题解使用返回值的符号来标识是否找到开始节点。
代码
/**
* @date 2024-04-24 8:56
*/
public class AmountOfTime2385 {
int startToParentToLeaf = 0;
int startToLeaf = 0;
int cnt = 0;
public int amountOfTime(TreeNode root, int start) {
dfs(root, start);
return Math.max(startToLeaf, startToParentToLeaf);
}
/**
* 返回子树深度
*/
public int[] dfs(TreeNode root, int start) {
if (root == null) {
return new int[]{0, 0};
}
int[] l = dfs(root.left, start);
int[] r = dfs(root.right, start);
boolean lfind = l[1] == 1;
boolean rfind = r[1] == 1;
int max = Math.max(r[0], l[0]);
if (lfind || rfind) {
startToParentToLeaf = Math.max(startToParentToLeaf, l[0] + r[0]);
// 这里的返回值不是max,而是祖先节点到开始节点的路径长度
return new int[]{(lfind ? l[0] : r[0]) + 1, 1};
}
if (root.val == start) {
startToLeaf = max;
// 这里直接返回1,不加max
// 视为将开始节点的左右子树删掉,后面回溯时直接相加左右子树高度即可
return new int[]{1, 1};
}
return new int[]{max + 1, 0};
}
/**
* 返回深度
*/
public int[] dfs_v1(TreeNode root, int start, int depth) {
if (root == null) {
return new int[]{depth - 1, 0};
}
int[] l = dfs_v1(root.left, start, depth + 1);
int[] r = dfs_v1(root.right, start, depth + 1);
boolean lfind = l[1] == 1;
boolean rfind = r[1] == 1;
int max = Math.max(r[0], l[0]);
if (lfind) {
cnt++;
startToParentToLeaf = Math.max(r[0] - depth + cnt, startToParentToLeaf);
}
if (rfind) {
cnt++;
startToParentToLeaf = Math.max(l[0] - depth + cnt, startToParentToLeaf);
}
if (root.val == start) {
startToLeaf = max - depth;
return new int[]{max, 1};
}
return new int[]{max, l[1] + r[1]};
}
}
性能
1052.爱生气的书店老板
目标
有一个书店老板,他的书店开了 n 分钟。每分钟都有一些顾客进入这家商店。给定一个长度为 n 的整数数组 customers ,其中 customers[i] 是在第 i 分钟开始时进入商店的顾客数量,所有这些顾客在第 i 分钟结束后离开。
在某些时候,书店老板会生气。 如果书店老板在第 i 分钟生气,那么 grumpy[i] = 1,否则 grumpy[i] = 0。
当书店老板生气时,那一分钟的顾客就会不满意,若老板不生气则顾客是满意的。
书店老板知道一个秘密技巧,能抑制自己的情绪,可以让自己连续 minutes 分钟不生气,但却只能使用一次。
请你返回 这一天营业下来,最多有多少客户能够感到满意 。
示例 1:
输入:customers = [1,0,1,2,1,1,7,5], grumpy = [0,1,0,1,0,1,0,1], minutes = 3
输出:16
解释:书店老板在最后 3 分钟保持冷静。
感到满意的最大客户数量 = 1 + 1 + 1 + 1 + 7 + 5 = 16.示例 2:
输入:customers = [1], grumpy = [0], minutes = 1
输出:1说明:
- n == customers.length == grumpy.length
- 1 <= minutes <= n <= 2 * 10^4
- 0 <= customers[i] <= 1000
- grumpy[i] == 0 or 1
思路
这道题要我们求满意顾客的最大值,老板会在指定的分钟生气,生气时,当前进入的顾客就会不满意,老板可以有一次忍耐的机会在一段时间内不生气。
刚开始想复杂了,以为顾客不是马上离开,而是在i分钟后离开。其实是第i分钟结束的时候就离开了。
因此,我们只需要计算老板忍耐的时间内,原本生气影响的顾客最大值,然后再加上不生气时的顾客总数即可。
这就是一个滑动窗口问题,窗口大小为忍耐时间,记录窗口内的不满意顾客的最大值。
这里面可以优化的点是使用乘法来代替条件判断,这样可以避免分支预测失败导致额外的性能损失。
代码
/**
* @date 2024-04-23 8:40
*/
public class MaxSatisfied1052 {
public int maxSatisfied_v1(int[] customers, int[] grumpy, int minutes) {
int n = customers.length;
int total = 0;
for (int i = 0; i < n; i++) {
total += customers[i] * (1 - grumpy[i]);
}
int unsatisfiedInWindow = 0;
for (int i = 0; i < minutes; i++) {
unsatisfiedInWindow += customers[i] * grumpy[i];
}
int max = unsatisfiedInWindow;
for (int i = minutes; i < n; i++) {
unsatisfiedInWindow = unsatisfiedInWindow
- customers[i - minutes] * grumpy[i - minutes]
+ customers[i] * grumpy[i];
max = Math.max(max, unsatisfiedInWindow);
}
return total + max;
}
}
性能
377.组合总和 Ⅳ
目标
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。请注意,顺序不同的序列被视作不同的组合。
题目数据保证答案符合 32 位整数范围。
示例 1:
输入:nums = [1,2,3], target = 4
输出:7
解释:
所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)示例 2:
输入:nums = [9], target = 3
输出:0说明:
- 1 <= nums.length <= 200
- 1 <= nums[i] <= 1000
- nums 中的所有元素 互不相同
- 1 <= target <= 1000
进阶:如果给定的数组中含有负数会发生什么?问题会产生何种变化?如果允许负数出现,需要向题目中添加哪些限制条件?
思路
这个题要求满足条件的排列数,从给定数组中选择任意数字,同一数字可以重复选择,使所选序列的和等于target。
首先初始化给定数组的dp,然后遍历0~target,计算dp。
代码
/**
* @date 2024-04-22 8:31
*/
public class CombinationSum377 {
public int combinationSum4(int[] nums, int target) {
Arrays.sort(nums);
int[] dp = new int[target + 1];
for (int i = 0; i < nums.length; i++) {
if (nums[i] <= target) {
dp[nums[i]] = 1;
}
}
for (int i = 0; i <= target; i++) {
for (int num : nums) {
if (i - num >= 0) {
dp[i] += dp[i - num];
}
}
}
return dp[target];
}
}
性能
216.组合总和 III
目标
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
- 只使用数字1到9
- 每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。示例 3:
输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字,我们可以得到的最小和是1+2+3+4 = 10,因为10 > 1,没有有效的组合。说明:
- 2 <= k <= 9
- 1 <= n <= 60
思路
从1~9中选k个,使它们的和是n。暴力求解需要 C9k 次遍历,可以使用回溯算法成批地考察具有特定前缀的所有候选解,一旦发现与目标解不合,需要撤销当前选择返回上一层进行下一个可能的尝试。dfs只是回溯算法的一环。关于回溯算法具体可参考《数据结构与算法分析》第314页。
代码
/**
* @date 2024-04-21 20:44
*/
public class CombinationSum216 {
public List<List<Integer>> combinationSum3(int k, int n) {
List<List<Integer>> res = new ArrayList<>();
Deque<Integer> q = new ArrayDeque<>();
for (int i = 1; i <= 9; i++) {
dfs(k - 1, i, n, q, res);
}
return res;
}
public void dfs(int k, int root, int target, Deque<Integer> q, List<List<Integer>> res) {
if (k < 0 || target < 0) {
return;
}
if (target == root && k == 0) {
q.offer(root);
res.add(new ArrayList<>(q));
q.pollLast();
return;
}
q.offer(root);
for (int i = root + 1; i <= 9; i++) {
dfs(k - 1, i, target - root, q, res);
}
q.pollLast();
}
}
性能