目标
树是一个无向图,其中任何两个顶点只通过一条路径连接。 换句话说,任何一个没有简单环路的连通图都是一棵树。
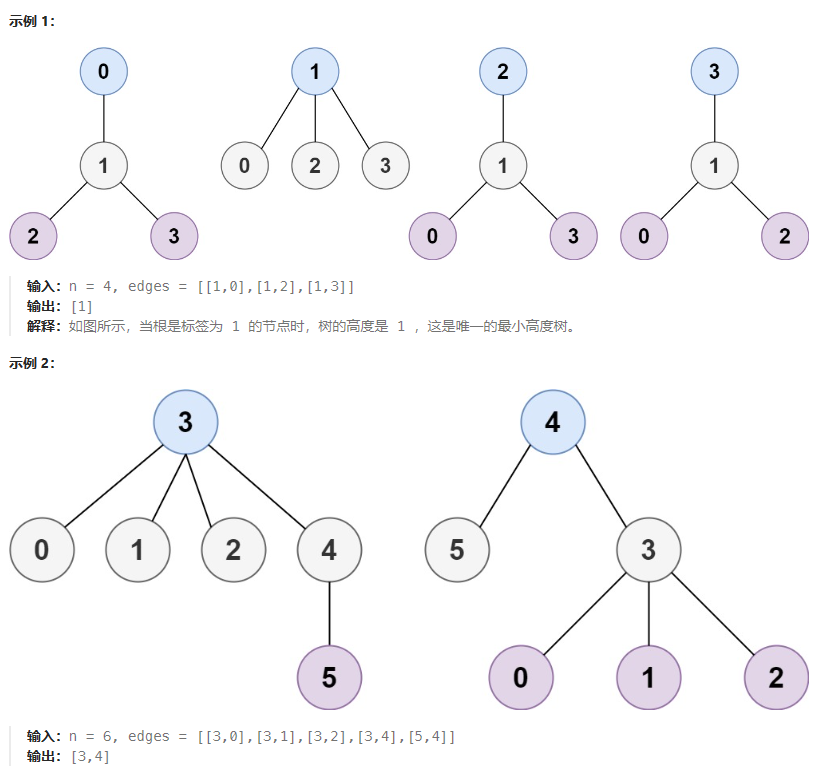
给你一棵包含 n 个节点的树,标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表(每一个边都是一对标签),其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。
可选择树中任何一个节点作为根。当选择节点 x 作为根节点时,设结果树的高度为 h 。在所有可能的树中,具有最小高度的树(即,min(h))被称为 最小高度树 。
请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。
树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。
说明:
- 1 <= n <= 2 * 10^4
- edges.length == n - 1
- 0 <= ai, bi < n
- ai != bi
- 所有 (ai, bi) 互不相同
- 给定的输入 保证 是一棵树,并且 不会有重复的边
思路
一看到这个题目就想起了换根动态规划,参考2581_统计可能的树根数目。
这个题是medium,但是感觉比上面参考那个hard题难多了,状态转换方程很难想。基本都是靠错误案例调试出来的。最开始写的dp方法调试了好几个小时,测试通过但是超时。然后开始怀疑dp根本就没法解,因为换根后状态是变化的,需要动态调整高度,并且还要区分当前节点是否为原来的根提供了最大高度。结果改到最后和暴力解法差不多了。
这种解法的关键是弄清楚换根之后节点高度的变化。经过分析只有换根的两个节点受到影响。分为两种情况,如果新根为旧根提供了最大高度,那么旧根应变为其邻接节点次大高度+1(第一次递归进来时计算)。如果新根没有为旧根提供最大高度,旧根高度不变仍为其邻接节点最大高度+1(第一次递归进来时计算)。新根是其邻接节点最大高度+1(这里面包括了刚才改变高度的旧根)。
注意:这里每个节点记录的是以0为根进行dfs,从叶子节点累加的高度。因此,当前节点高度就等于邻接节点最大高度加1。
代码
/**
* @date 2024-03-17 16:04
*/
public class FindMinHeightTrees {
public int[] res;
public int minHeight;
List<Integer>[] g;
int[] dp;
public List<Integer> findMinHeightTrees(int n, int[][] edges) {
g = new ArrayList[n];
for (int i = 0; i < g.length; i++) {
g[i] = new ArrayList<>();
}
dp = new int[n];
res = new int[n];
minHeight = n;
for (int i = 0; i < edges.length; i++) {
g[edges[i][0]].add(edges[i][1]);
g[edges[i][1]].add(edges[i][0]);
}
dfs(0, 0);
redfs(0, 0);
List<Integer> minHeights = new ArrayList<>();
for (int i = 0; i < n; i++) {
if (res[i] == minHeight) {
minHeights.add(i);
}
}
return minHeights;
}
public void redfs(int root, int parent) {
// 进入到该层后,保存其最大与次大深度,后面换根后再回来遍历其它兄弟节点时不会受到换根影响
// 由于是深度遍历,换根到子节点与当前根的深度有关
// 由子节点返回后,状态已保存,不受换根影响
int max = 0;
int second = 0;
for (Integer neighbor : g[root]) {
if (dp[neighbor] > max) {
second = max;
max = dp[neighbor];
} else if (dp[neighbor] > second) {
second = dp[neighbor];
}
}
// max是与root相邻节点的高度,加1才是root的最大高度
res[root] = max + 1;
// 更新最小高度
minHeight = Math.min(minHeight, res[root]);
for (Integer next : g[root]) {
if (next == parent) {
// 遇到叶子节点返回
continue;
}
// 换到下一个根next,修改root的高度,如果下一个点为当前点提供了最大高度,那么当前节点高度为
// 次高加一,否则是最高加一
dp[root] = (dp[next] == max ? second : max) + 1;
redfs(next, root);
}
}
public int dfs(int root, int parent) {
dp[root] = 1;
for (Integer next : g[root]) {
if (next != parent) {
dp[root] = Math.max(dp[root], dfs(next, root) + 1);
}
}
return dp[root];
}
public static void main(String[] args) {
FindMinHeightTrees main = new FindMinHeightTrees();
// System.out.println(main.findMinHeightTrees(4, new int[][]{{1, 0}, {1, 2}, {1, 3}}));
// System.out.println(main.findMinHeightTrees(6, new int[][]{{3, 0}, {3, 1}, {3, 2}, {3, 4}, {5, 4}}));
// System.out.println(main.findMinHeightTrees(7, new int[][]{{0, 1}, {1, 2}, {1, 3}, {2, 4}, {3, 5}, {4, 6}}));
// System.out.println(main.findMinHeightTrees(8, new int[][]{{0,1},{1,2},{2,3},{0,4},{4,5},{4,6},{6,7}}));
System.out.println(main.findMinHeightTrees(11, new int[][]{{0, 1}, {0, 2}, {2, 3}, {0, 4}, {2, 5}, {5, 6}, {3, 7}, {6, 8}, {8, 9}, {9, 10}}));
// System.out.println(main.findMinHeightTrees(2, new int[][]{{0, 1}}));
}
}
性能