日期: 2024 年 2 月 27 日

目标

给定二叉搜索树的根结点 root，返回值位于范围 [low, high] 之间的所有结点的值的和。

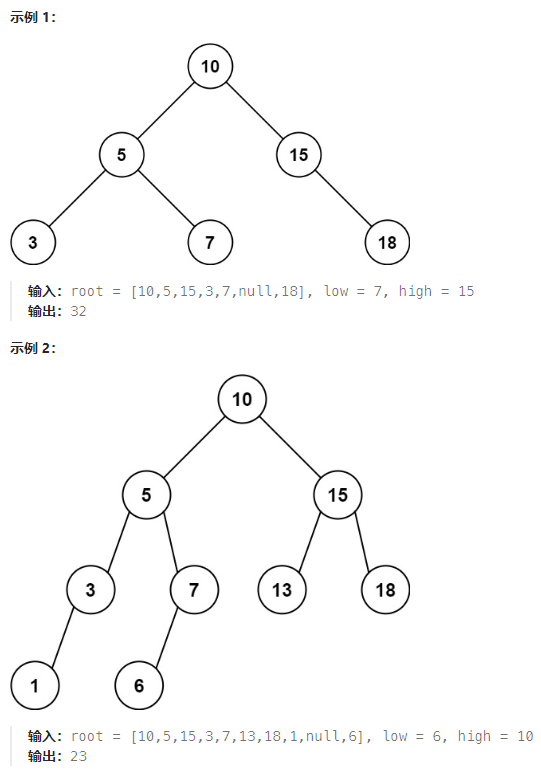
说明：

• 树中节点数目在范围 [1, 2 * 10^4] 内
• 1 <= Node.val <= 10^5
• 1 <= low <= high <= 10^5
• 所有 Node.val 互不相同

思路

二叉搜索树，也叫二叉查找树（Binary Search Tree, BST）。BST是一颗二叉树，其中的每个节点都含有一个可比较的Key，并且每个节点的Key都大于其左子树中的任意节点的Key，而小于其右子树的任意节点的Key。

比较每个节点是否在给定的范围内，如果节点Key小于low去左子树找，大于high则去右子树找，如果在二者之间，累加和，继续遍历左右子树。

代码

/**
 * @date 2024/2/26 10:37
 */
public class RangeSumBST {
    public class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode() {
        }

        TreeNode(int val) {
            this.val = val;
        }

        TreeNode(int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }

        @Override
        public String toString() {
            return "TreeNode{" +
                    "val=" + val +
                    ", left=" + left +
                    ", right=" + right +
                    '}';
        }
    }

    public int sum = 0;

    /** 省去了节点为空的判断嵌套*/
    public int rangeSumBST_v1(TreeNode root, int low, int high) {
        if (root == null) {
            return 0;
        }
        if (low > root.val) {
            rangeSumBST_v1(root.right, low, high);
        }
        if (high < root.val) {
            rangeSumBST_v1(root.left, low, high);
        }
        if (high >= root.val && low <= root.val) {
            sum += root.val;
            rangeSumBST_v1(root.left, low, high);
            rangeSumBST_v1(root.right, low, high);
        }
        return sum;
    }

    public int rangeSumBST(TreeNode root, int low, int high) {
        if (low > root.val) {
            if (root.right != null) {
                rangeSumBST(root.right, low, high);
            }
        }
        if (high < root.val) {
            if (root.left != null) {
                rangeSumBST(root.left, low, high);
            }
        }
        if (high >= root.val && low <= root.val){
            sum += root.val;
            if (root.left != null) {
                rangeSumBST(root.left, low, high);
            }
            if (root.right != null) {
                rangeSumBST(root.right, low, high);
            }
        }
        return sum;
    }
}

性能