2583.二叉树中的第K大层和

目标

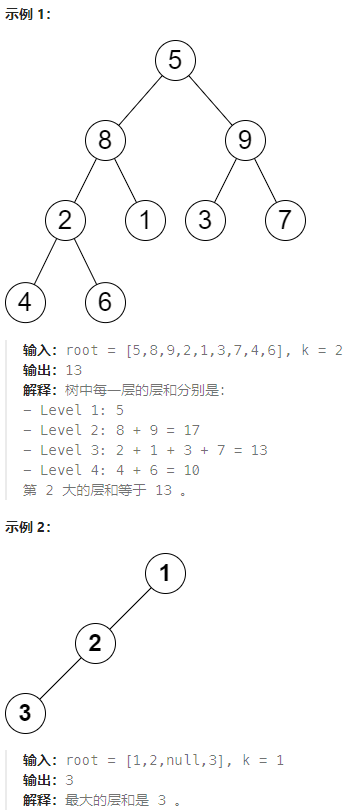
给你一棵二叉树的根节点 root 和一个正整数 k 。

树中的 层和 是指 同一层 上节点值的总和。

返回树中第 k 大的 层和（不一定不同）。如果树少于 k 层，则返回 -1 。

注意，如果两个节点与根节点的距离相同，则认为它们在同一层。

说明：

• 树中的节点数为 n
• 2 <= n <= 10^5
• 1 <= Node.val <= 10^6
• 1 <= k <= n

思路

这个问题的关键在于遍历的同时记录层数并进行累加。由于是升序排列所以取倒数第k个，即MAX-k。

代码

/**
 * @date 2024-02-23 16:06
 */
public class KthLargestLevelSum {
    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode() {
        }

        TreeNode(int val) {
            this.val = val;
        }

        TreeNode(int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }

        @Override
        public String toString() {
            return "TreeNode{" +
                    "val=" + val +
                    ", left=" + left +
                    ", right=" + right +
                    '}';
        }
    }

    public static void main(String[] args) {
        KthLargestLevelSum main = new KthLargestLevelSum();
        long res = main.kthLargestLevelSum(new TreeNode(1, new TreeNode(2), new TreeNode(3)), 2);
        System.out.println(res);
    }

    public final int MAX = 100000;
    public long[] lacc = new long[MAX];
    public int maxlevel = 0;

    public long kthLargestLevelSum(TreeNode root, int k) {
        traverseSubTree(root, 0);
        if (k > maxlevel + 1) {
            return -1;
        }
        Arrays.sort(lacc);
        return lacc[MAX-k];
    }
    public void traverseSubTree(TreeNode subTree, int level) {
        maxlevel = Math.max(maxlevel, level);
        lacc[level] += subTree.val;
        if (subTree.left != null) {
            traverseSubTree(subTree.left, level + 1);
        }
        if (subTree.right != null) {
            traverseSubTree(subTree.right, level + 1);
        }
    }
}

Arrays.sort使用的是双轴快排(DualPivotQuicksort)，时间复杂度是O(nlogn)。

性能

最优的算法是快速选择。因为我们并不需要所有的元素都有序，只要保证k位置的左侧都比k小，右侧均比k大即可，而两侧区间内部是不需要排序的。