目标
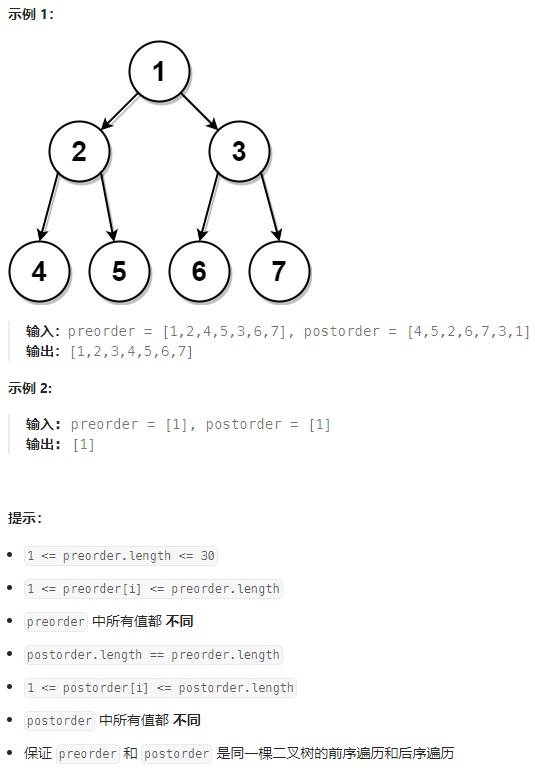
给定两个整数数组,preorder 和 postorder ,其中 preorder 是一个具有 无重复 值的二叉树的前序遍历,postorder 是同一棵树的后序遍历,重构并返回二叉树。
如果存在多个答案,您可以返回其中 任何 一个。
思路
本来看到这个题目觉得没什么新意,前面都已经做过 从前序与中序遍历序列构造二叉树 与 从中序与后序遍历序列构造二叉树这两个题目了,准备快速写一下。没想到,又花费了许多时间。虽然知道大体的方向,但真正写出来还是不那么容易的。对照着一个案例,按照大体思路写完解决方法之后,就急着去测试,结果有的例没有通过,有的数组越界。然后就开始调试,一会这加个判断,那处理一个特例,这个案例通过了,别的又不行了,一来二去就把自己绕晕了。之所以存在这样的情况还是对这个问题的理解不到位,没有一个清晰的思路。
有了前面的两道题的求解经验,我们知道这个题还是用递归求解更容易一些。求解的核心是遍历先序/后序序列,一个从前向后,一个从后向前。将遍历到的每一个节点去中序序列中找到相应位置然后划分左/右子树,然后递归处理子树。其实这里容易忽略一个问题,就是左/子树的节点一定会在先序/后序序列随后遍历中出现。可以根据这个来明确临界条件,否则容易漏掉或者弄错左右以及父节点。这也就是为什么先序序列先遍历左子树,后序先遍历右子树的原因。因为游标顺序移动,刚好可以覆盖相应的子树。刚开始我还想着分别在先序和后序维护两个游标,这是不可行的。
说回到这个题目,它不像前面两个那样可以明确左右子树。前面说前序序列的第二个节点是其左子树或右子树的根节点,并非是无法确定,而是需要结合实际情况看是否存在左子树,如果存在则一定是左子树根节点。这个可以在中序序列中找到相应位置就知道了。但是对于这个题而言左右是无法确定的,很简单的例子 [1,2] 与 [2,1]。
我们的思路是遍历先序序列,找到其在后序序列的位置,该位置减1则是可能的右根节点,反查其在先序序列中的位置。这样我们就得到了一个左子树区间或者单个节点(无法确定左右)。这样我们就可以递归构建左子树,对于单个节点的情况需要将搜索范围扩展到序列结尾,否则可能反查不到节点在先序序列中的位置。
代码
/**
* @date 2024-02-23 10:05
*/
public class BuildBinaryTreeFromPrePost {
public static class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
@Override
public String toString() {
return "TreeNode{" +
"val=" + val +
", left=" + left +
", right=" + right +
'}';
}
}
public static int preCursor = 1;
public static void main(String[] args) {
BuildBinaryTreeFromPrePost main = new BuildBinaryTreeFromPrePost();
// int[] preorder = new int[]{1,2,4,5,3,6,7};
// int[] preorder = new int[]{3, 9, 20, 15, 7};
// int[] preorder = new int[]{1,2};
// int[] preorder = new int[]{2,1,3};
// int[] preorder = new int[]{4,2,1,3};
int[] preorder = new int[]{3,4,2,1};
// int[] preorder = new int[]{1};
// int[] postorder = new int[]{4,5,2,6,7,3,1};
// int[] postorder = new int[]{1};
// int[] postorder = new int[]{9, 15, 7, 20, 3};
// int[] postorder = new int[]{2,1};
// int[] postorder = new int[]{3,1,2};
// int[] postorder = new int[]{3,1,2,4};
int[] postorder = new int[]{2,1,4,3};
System.out.println(main.constructFromPrePost(preorder, postorder));
}
public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
TreeNode root = new TreeNode(preorder[0]);
if (preorder.length == 1) {
return root;
}
int rightRootPreIndex = 0;
for (int i = 0; i < preorder.length; i++) {
if (postorder[postorder.length - 2] == preorder[i]){
rightRootPreIndex = i;
break;
}
}
// 注意当start == end时,搜索长度应扩展到整个数组长度,否则会导致查询不到当前节点的右子树根节点。
root.left = buildSubTree(preorder, postorder, preCursor, rightRootPreIndex == preCursor ? preorder.length:rightRootPreIndex);
if (preCursor >= rightRootPreIndex && preCursor < preorder.length) {
root.right = buildSubTree(preorder, postorder, rightRootPreIndex, preorder.length);
}
return root;
}
public TreeNode buildSubTree(int[] preorder, int[] postorder, int start, int end){
TreeNode root = new TreeNode(preorder[preCursor]);
int rightRootPostIndex = 0;
int rightRootPreIndex = 0;
for (int i = 0; i < postorder.length; i++) {
if (root.val == postorder[i]){
rightRootPostIndex = i;
preCursor++;
break;
}
}
if (rightRootPostIndex > 0) {
for (int i = start; i < end; i++) {
if (postorder[rightRootPostIndex - 1] == preorder[i]) {
rightRootPreIndex = i;
break;
}
}
if (preCursor < rightRootPreIndex) {
root.left = buildSubTree(preorder, postorder, preCursor, rightRootPreIndex == 0 ? preorder.length : rightRootPreIndex);
}
if (preCursor >= rightRootPreIndex && preCursor < end && rightRootPreIndex !=0) {
root.right = buildSubTree(preorder, postorder, rightRootPreIndex, end);
}
}
return root;
}
}先序序列的初始条件是直接从第二个位置开始的,直接从后序序列的倒数第二个反查其在先序序列的位置。
性能