106.从中序与后序遍历序列构造二叉树

目标

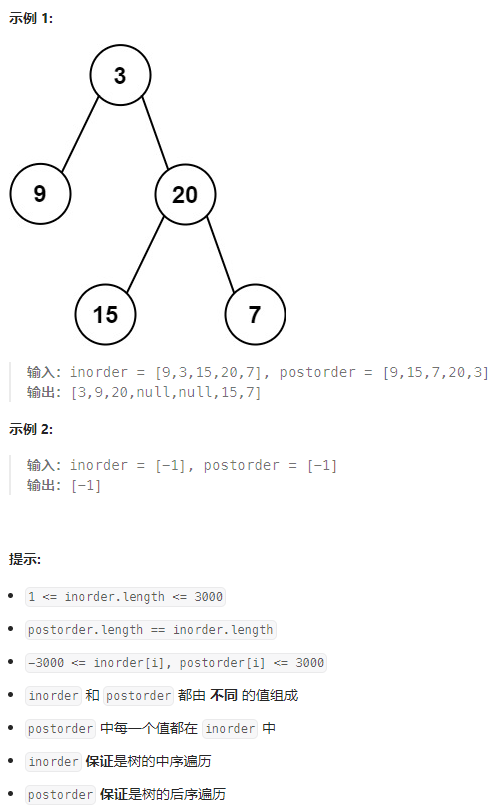
给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

思路

有了前面 从前序与中序遍历序列构造二叉树 的经验这个问题就很好处理了。二叉树的后序遍历指先访问左子树、再访问右子树，最后访问根节点。

只需从后序序列的最后一个元素向前遍历即可，最后一个是根节点，接着是右子树、左子树的根节点 （注意这里是先右后左）。

还是在中序遍历中找到该根节点，然后其左侧的为左子树，右侧为右子树。依次递归遍历右子树与左子树，在递归方法中根节点取后序序列的前一个节点即可。

代码

/**
 * @date 2024-02-21 14:12
 */
public class BuildBinaryTreeFromMidPost {
    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode() {
        }

        TreeNode(int val) {
            this.val = val;
        }

        TreeNode(int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }

        @Override
        public String toString() {
            return "TreeNode{" +
                    "val=" + val +
                    ", left=" + left +
                    ", right=" + right +
                    '}';
        }
    }

//    static int[] inorder = new int[]{9, 3, 15, 20, 7};
    static int[] inorder = new int[]{2,3,1};
//    static int[] inorder = new int[]{-1};

//    static int[] postorder = new int[]{9, 15, 7, 20, 3};
    static int[] postorder = new int[]{3,2,1};
//    static int[] postorder = new int[]{-1};

    static int postCursor = postorder.length - 1;

    public static void main(String[] args) {
        int rootIndex = 0;
        TreeNode root = new TreeNode(postorder[postCursor]);
        for (int i = 0; i < inorder.length; i++) {
            if (inorder[i] == postorder[postCursor]) {
                rootIndex = i;
                // 一定能够找到
                postCursor--;
                break;
            }
        }
        int leftEndIndex = rootIndex - 1;
        int rightStartIndex = rootIndex + 1;
        // 注意这个postCursor应该是共享变量，原先是想以参数传递的，但是发现递归的时候还要将它传回来，改成了共享变量
        // 这里是先遍历右子树再左子树
        if (rightStartIndex < inorder.length) {
            root.right = traverseSubTree(inorder, rightStartIndex, inorder.length);
        }
        if (leftEndIndex >= 0) {
            root.left = traverseSubTree(inorder, 0, leftEndIndex);
        }
        System.out.println(root);
    }

    public static TreeNode traverseSubTree(int[] inorder, int start, int end) {
        TreeNode subRoot = new TreeNode(postorder[postCursor]);
        int rootIndex = start;
        for (int i = start; i <= end; i++) {
            if (inorder[i] == postorder[postCursor]) {
                rootIndex = i;
                postCursor--;
                break;
            }
        }
        int leftEndIndex = rootIndex - 1;
        int rightStartIndex = rootIndex + 1;
        // 临界条件判断，这里应该是<=，并且排除掉inorder.length
        // 这里是先遍历右子树再左子树
        if (rightStartIndex <= end && rightStartIndex != inorder.length) {
            // 这里的结束条件传end
            subRoot.right = traverseSubTree(inorder, rightStartIndex, end);
        }
        if (leftEndIndex >= start) {
            subRoot.left = traverseSubTree(inorder, start, leftEndIndex);
        }
        return subRoot;
    }
}

性能