105.从前序与中序遍历序列构造二叉树

目标

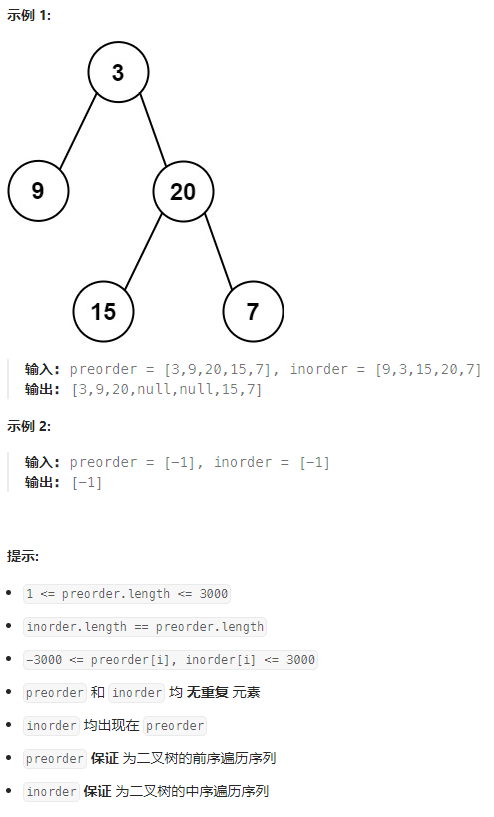
给定两个整数数组 preorder 和 inorder，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

思路

首先要明白先序遍历与中序遍历的概念。所谓二叉树的 先序遍历 指的是 先访问根节点，然后遍历左子树，再遍历右子树。中序遍历 则是 先遍历左子树，再根节点，然后右子树。

很容易想到使用递归，关键点是数组左右边界的维护，临界条件的判断。

注意到 先序遍历数组的第一个节点一定是根节点，其后面的节点则是其左子树或右子树的根节点。

于是先根据根节点在中序遍历中找到该根节点，然后其左侧的为左子树，右侧为右子树。依次递归遍历左子树与右子树（注意判断边界条件），在递归方法中根节点取刚才根节点的后一个节点（需要一个共享变量来记录位置）。

代码

/**
 * @date 2024-02-20 11:43
 */
public class BuildBinaryTree {

    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode() {
        }

        TreeNode(int val) {
            this.val = val;
        }

        TreeNode(int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }

        @Override
        public String toString() {
            return "TreeNode{" +
                    "val=" + val +
                    ", left=" + left +
                    ", right=" + right +
                    '}';
        }
    }

    static int[] preorder = new int[]{3, 9, 20, 15, 7};
//    static int[] preorder = new int[]{1,2,3};
//    static int[] preorder = new int[]{-1};

    static int[] inorder = new int[]{9, 3, 15, 20, 7};
//    static int[] inorder = new int[]{2,3,1};
//    static int[] inorder = new int[]{-1};

    static int preCursor = 0;

    public static void main(String[] args) {
        int rootIndex = 0;
        TreeNode root = new TreeNode(preorder[preCursor]);
        for (int i = 0; i < inorder.length; i++) {
            if (inorder[i] == preorder[preCursor]) {
                rootIndex = i;
                // 一定能够找到
                preCursor++;
                break;
            }
        }
        int leftEndIndex = rootIndex - 1;
        int rightStartIndex = rootIndex + 1;
        if (leftEndIndex >= 0) {
            root.left = traverseSubTree(inorder, 0, leftEndIndex);
        }
        // 注意这个preCursor应该是共享变量
        if (rightStartIndex < inorder.length) {
            root.right = traverseSubTree(inorder, rightStartIndex, inorder.length);
        }
        System.out.println(root);
    }

    public static TreeNode traverseSubTree(int[] inorder, int start, int end) {
        TreeNode subRoot = new TreeNode(preorder[preCursor]);
        int rootIndex = start;
        for (int i = start; i <= end; i++) {
            if (inorder[i] == preorder[preCursor]) {
                rootIndex = i;
                preCursor++;
                break;
            }
        }
        int leftEndIndex = rootIndex - 1;
        int rightStartIndex = rootIndex + 1;
        if (leftEndIndex >= start) {
            subRoot.left = traverseSubTree(inorder, start, leftEndIndex);
        }
        // 临界条件判断，这里应该是<=，并且排除掉inorder.length
        if (rightStartIndex <= end && rightStartIndex != inorder.length) {
            // 这里的结束条件传end
            subRoot.right = traverseSubTree(inorder, rightStartIndex, end);
        }
        return subRoot;
    }
}

性能

我的目标是能解决问题就好，看了下性能分布还有优化的空间，官网还给出了迭代的解法，没时间看。递归应该是更容易理解的方法了。希望能够坚持下去吧。